La logica della segnalazione causale-foliata
La teoria di Segnalazione causale-foliata (CFS) propone che il tempo contenga strati nascosti che consentono una coerenza limitata più veloce della luce tra sistemi quantistici. I ricercatori potrebbero presto utilizzare Transistor ad accoppiamento quantistico (QCT) – un nanodispositivo a doppio grafene – per testare direttamente questi effetti e determinare se possono verificarsi senza violare le leggi note della fisica.
In sostanza, la CFS pone una domanda provocatoria: E se alcuni tipi di onde, come i campi evanescenti o vicini, potessero condividere informazioni di fase più velocemente della luce, pur mantenendo la causalità?
Se così fosse, lo spaziotempo potrebbe non essere perfettamente uniforme. Potrebbe contenere una sottile struttura interna – una "stratificazione" del tempo, in cui le informazioni avanzano leggermente all'interno di ogni strato, pur rimanendo coerenti nel complesso.

In questa prospettiva, l'universo si dispiega come le pagine di un immenso libro cosmico: ogni pagina si gira in perfetto ordine, anche se alcune si girano un po' più velocemente di altre. La CFS offre una visione raffinata della relatività, che consente una coerenza superluminale strutturata mantenendo intatta la storia di causa ed effetto.
Parte II. Segnalazione causale-foliata (CFS)
- Assiomi fondamentali
- Cinematica e Dinamica
- Regole quantistiche e conservazione
- Previsioni sperimentali
- Protocolli di prova
- Ruolo del QCT
1. Assiomi fondamentali
- Foliazione temporale globale: Lo spaziotempo possiede una suddivisione globale preferita (tempo cosmico, definito dal vettore di tipo tempo uᵃ). Tutti i segnali, luminali e superluminali, sono ordinati da questa foliazione.
- Cono di segnale ingrandito: Oltre al cono di luce, esiste un “cono di segnale” più ampio per specifici media o campi (χ).
- Protezione cronologica: I cicli di segnale chiusi sono dinamicamente proibiti dai vincoli di risolvibilità.
- Località operativa: Gli esperimenti standard rimangono invarianti rispetto a Lorentz; le deviazioni si verificano solo all'interno dei mezzi abilitati.
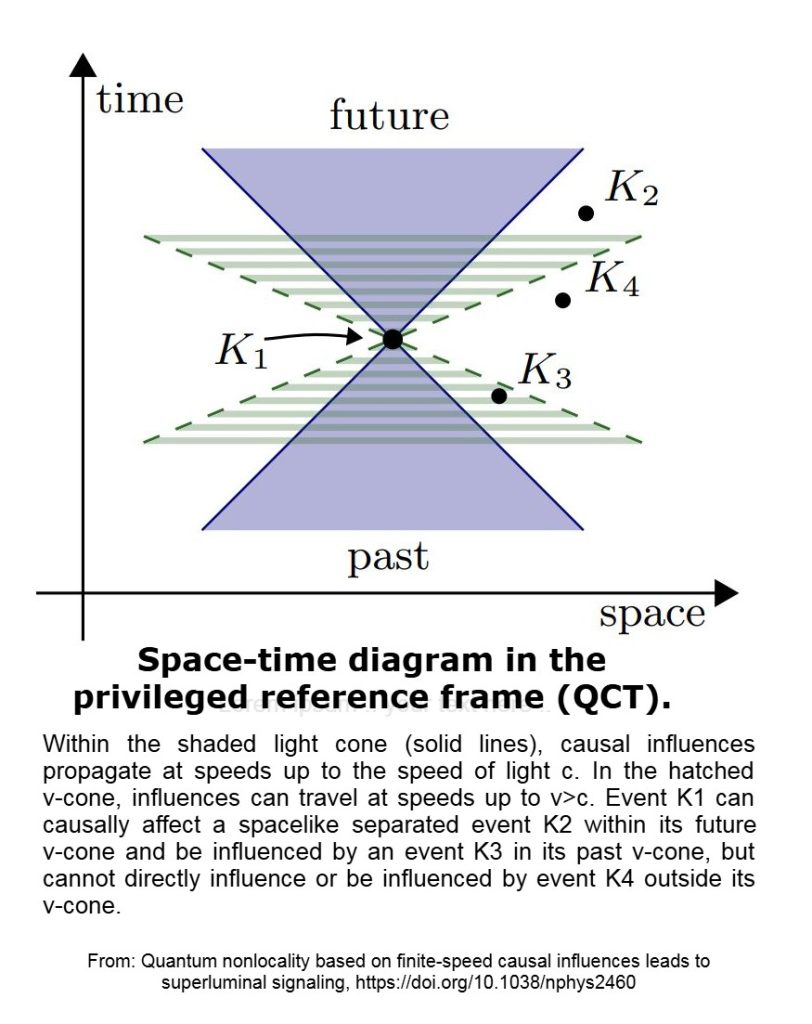
2. Cinematica e dinamica
- Cornice preferita: Allineato approssimativamente con il telaio di appoggio della CMB.
- Campo del segnale (χ): Si accoppia debolmente ai portatori EM, ampliando il cono causale.
- Caratteristiche superluminali: EDP nei media abilitati la propagazione avviene al di fuori del cono di luce g.
- Vincolo No-Loop: Le condizioni integrali impediscono cicli causali che diminuiscono il tempo.
3. Regole quantistiche e conservazione
Abbiamo costruito una piccola regione (il gap QCT) dove i campi quantistici vicini possono essere delicatamente modellati in modo che un campo appena rilevabile, più veloce della luce modello si manifesta in dati altrimenti casuali, sufficientemente piccoli da garantire la sicurezza della fisica e sufficientemente chiari da poter essere testati in laboratorio.

Se la dichiarazione compatta sopra ti sembra sensata, puoi espandere la parte evidenziata in rosso Regole quantistiche qui sotto cliccando sui triangoli neri ▶, per una discussione PIÙ dettagliata.
Per i lettori comuni, ogni sezione include una breve spiegazione (senza calcoli matematici) seguita da un'analogia. Sebbene la maggior parte delle persone non ne abbia mai sentito parlare, teorema di non comunicazione (proibire la comunicazione più veloce della luce… tramite entanglement), è qui posto in evidenza per la sua importanza fondamentale, e perché un controllata relax di quella regola viene esplorato qui.
[clicca per aprire] Teorema di non comunicazione rilassato: Nei media abilitati, le dinamiche non lineari/post-selezionate consentono una capacità classica minima > 0.
Richiesta (operativa):
In un mezzo abilitato (ad esempio, un gap QCT che agisce come campo vicino abilitato χ), a debole non linearità localizzata or post-selezione esplicita può produrre a capacità classica piccola ma finita C>0 tra parti separate dallo spazio senza violare l'unitarietà globale o la regola di Born.
Impostare
lasciare ρAB essere uno stato bipartito condiviso da Alice e Bob. Nella meccanica quantistica standard con stato locale Mappe CPTP e no dopo la selezione, lo stato ridotto di Bob è indipendente dalla scelta di Alice:
ρB′=TrA[(ΦA⊗IB)(ρAB)]=ρB, (nessuna segnalazione)
In un abilitato Regione QCT, modello dell'operazione controllata di Alice come un debolmente non lineare perturbazione di un Mappa CPTP:
ΦA(V)(⋅)=ΛA(⋅)+ε\mathcal{N}_A^{(V)}[⋅], 0<ε≪1,[/latex] dove [latex]V è il controllo di Alice (ad esempio, la distorsione interstrato), LA è CPTP e \mathcal{N}_A^{(V)} è un funzionale non lineare limitato attivo solo all'interno dell' χ-supporto abilitato.Lo stato di Bob diventa
ρB′(V)=TrA[(ΦA(V)⊗IB)ρAB]=ρB(0)+εΔρB(V),con
ΔρB(V)=TrA [(NA(V)⊗IB)ρAB].\Delta\rho_B(V)=\mathrm{Tr}_A\!\Big[\big(\mathcal{N}_A^{(V)}\otimes \mathbb{I}_B\big)\rho_{AB}\Big].ΔρB(V)=TrA[(NA(V)⊗IB)ρAB].
If \Delta\rho_B(V_0)\neq \Delta\rho_B(V_1), allora le statistiche dei risultati di Bob dipendono (leggermente) dalla scelta di Alice V, consentendo la comunicazione classica all'ordine \varepsilon.
Per un POVM \{Mio\} su Bob, le probabilità di rilevamento sono
P(y∣V)=Tr[MyρB′(V)]=P0(y)+εΔP(y∣V),ΔP(y∣V):=Tr[MyΔρB(V)].Capacità con segnalazione debole
Lascia che Alice invii un simbolo binario X\in\{0,1\} Scegliendo V\in\{V_0,V_1\}.Bob misura Y\in\{0,1\}. Definire
\delta := P(Y=1\mid V_1)-P(Y=1\mid V_0)=\varepsilon\,\Delta P + O(\varepsilon^2),con probabilità di errore di base p:=P(Y=1∣V0).
Per un canale con input binario e output binario nel limite di piccolo segnale ∣\delta|\ll 1, l' Capacità di Shannon ammette l'approssimazione quadratica
C \;\approx\; \frac{\delta^2}{2\ln 2}\,\frac{1}{p(1-p)} \;+\; O(\delta^4), \qquad C>0\ \text{se e solo se}\ \delta\neq 0.
Quindi qualsiasi diverso da zero \delta (quindi qualsiasi diverso da zero \varepsilon- dipendenza dall'ordine V) produce un finito C>0.
Ruolo della post-selezione
Se Bob (o un circuito di coincidenza congiunto) post-seleziona su una finestra di risultato W con probabilità di successo pW, l' condizionale lo stato è
\rho_{B\!\mid W}(V)\;=\;\frac{\Pi_W\,\rho_B'(V)\,\Pi_W}{\mathrm{Tr}\!\big[\Pi_W\,\rho_B'(V)\big]}, \qquad \Pi_W=\Pi_W^\dagger=\Pi_W^2.A causa della normalizzazione da parte \mathrm{Tr}[\Pi_W\rho_B'(V)], la mappatura \rho'_B \mapsto \rho_B^{\mid W} is non lineare, e le statistiche condizionate possono acquisire un V-dipendenza anche quando il incondizionato l'uguaglianza senza segnalazione è valida. In pratica, la post-selezione scala il tasso utile di pW:
C_{\mathrm{eff}} \approx p_W , C.Condizioni di coerenza
Per evitare patologie globali:
- Localizzazione: \mathcal{N}_A^{(V)} è limitato al χ-regione abilitata (ad esempio, il gap QCT).
- Piccolezza: \varepsilon è sufficientemente piccolo da preservare la stabilità e i limiti energetici.
- Unitarietà globale e regola di Born: La dinamica dell'insieme rimane CPTP; eventuali deviazioni sono limitate alle mappe del rivelatore locale condizionato (post-selezione) o al settore debole-non lineare all'interno del mezzo.
Dichiarazione compatta
\boxed{ \begin{aligned} &\Phi_A^{(V)}=\Lambda_A+\varepsilon\,\mathcal{N}_A^{(V)},\quad \varepsilon\ll 1,\\ &\rho_B'(V)=\rho_B^{(0)}+\varepsilon\,\Delta\rho_B(V),\quad \Delta\rho_B(V)=\mathrm{Tr}_A\!\big[(\mathcal{N}_A^{(V)}\!\otimes\!\mathbb{I})\,\rho_{AB}\big],\\ &\esiste\,M:\ \delta=\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_1)\big]-\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_0)\big]\neq 0 \\ &\Rightarrow\ C \approx \dfrac{\delta^2}{2\ln 2\, p(1-p)} \;>\;0,\quad C_{\text{eff}}\approx p_W\,C\ \text{(con post-selezione)}. \end{aligned}}Ecco una ripartizione e una verifica dei fatti della compatta affermazione matematica:
L'enunciato matematico è la rappresentazione di un risultato nella teoria dell'informazione quantistica, correlato al calcolo della capacità di un canale quantistico con una piccola perturbazione. Collega la descrizione fisica di un canale quantistico alla capacità del canale risultante, incorporando concetti come la perturbazione di stato, la distinguibilità degli stati di uscita e l'effetto della post-selezione. Analizziamo ogni parte per verificarne i componenti:
Perturbazione del canale e dello stato
\Phi_A(V) = \Lambda_A + \epsilon N_A(V), \epsilon \ll 1: Questo descrive un canale quantistico \Phi_A agendo su un sistema A. Esso è costituito da una parte dominante e costante \Lambda_A e una piccola perturbazione \epsilon N_A(V)Durante la serata, \epsilon è un parametro piccolo e V è un parametro controllabile del canale. Questo è un modo standard per rappresentare un canale quantistico leggermente modulato o rumoroso. \rho_B'(V) = \rho_B(0) + \epsilon \Delta\rho_B(V): Questo mostra l'effetto del canale su una parte di uno stato quantistico più ampio. Indica che lo stato di uscita di un sottosistema B, \rho_B'(V), è una versione leggermente perturbata di uno stato iniziale \rho_B(0)La perturbazione \Delta\rho_B(V) è proporzionale al parametro piccolo \epsilon. \Delta\rho_B(V) = Tr_A[(N_A(V) \otimes I)\rho_{AB}]: Questa è la forma esplicita della perturbazione del primo ordine allo stato del sistema B. Si ricava prendendo la traccia parziale (Tr_A) sul sistema A dell'azione della parte perturbativa del canale su uno stato più grande e aggrovigliato \rho_{AB}Questa è un'applicazione standard e corretta delle regole della meccanica quantistica.
Distinguibilità degli stati
\esiste M: \delta = \epsilon Tr[M\Delta\rho_B(V_1)] - \epsilon Tr[M\Delta\rho_B(V_0)] \neq 0: Questo è il passaggio cruciale per stabilire una capacità del canale diversa da zero. Afferma che esiste un operatore di misura (un operatore hermitiano) M in grado di distinguere tra gli stati perturbati corrispondenti a due diverse impostazioni del parametro del canale, V_1 e V_0La quantità \delta rappresenta la differenza nel valore atteso della misura M per i due stati di uscita. Il fatto che \delta \neq 0 è la condizione affinché i due stati siano sperimentalmente distinguibili, almeno in linea di principio.
Capacità del canale
C \approx \frac{\delta^2}{2\ln{2}p(1-p)} > 0: Questo è un risultato chiave, probabilmente un'approssimazione per la capacità di Holevo o una misura correlata della capacità del canale nel limite di piccole \deltaLa capacità C è una misura della velocità massima alla quale le informazioni possono essere inviate in modo affidabile attraverso il canale. Il termine \delta^2 è previsto, poiché la capacità spesso scala con il quadrato della distinguibilità degli stati di uscita per piccole perturbazioni. Il fattore di 2\ln{2} è lo standard per la conversione da unità naturali di informazione (nat) a bit. Il termine p(1-p) nel denominatore suggerisce che la capacità viene valutata per uno specifico insieme di input, dove i due stati (corrispondenti a V_0 e V_1) vengono utilizzati con probabilità p e 1-p. La capacità è massimizzata quando p=1/2, che è un presupposto comune.
Capacità effettiva con post-selezione
C_{eff} \approx p_W C (con post-selezione): questa parte dell'affermazione descrive la capacità effettiva quando si utilizza la post-selezione. La post-selezione è una tecnica in cui viene considerato solo un sottoinsieme dei risultati della misurazione, il che a volte può amplificare un segnale debole. p_W sarebbe la probabilità di una post-selezione di successo (la "probabilità di post-selezione"). La capacità effettiva C_{eff} è ridotto di questa probabilità perché molti degli stati iniziali vengono scartati. Questo è un compromesso ben noto negli schemi di post-selezione: si potrebbe ottenere un segnale più chiaro, ma si perde una porzione significativa dei dati, riducendo così la velocità complessiva di trasmissione delle informazioni.
Verifica dei fatti sull'intelligenza artificiale: conclusione
Le espressioni matematiche sono coerenti con i principi consolidati della teoria dell'informazione quantistica. La logica scorre correttamente dalla definizione di un canale quantistico perturbato alla distinguibilità dei suoi stati di uscita e, infine, a un'espressione per la capacità del canale. Anche l'inclusione dell'effetto della post-selezione è standard. Pertanto, la matematica nell'enunciato compatto sembra essere corretta e rappresenta una valida linea di ragionamento nel contesto della capacità del canale quantistico.
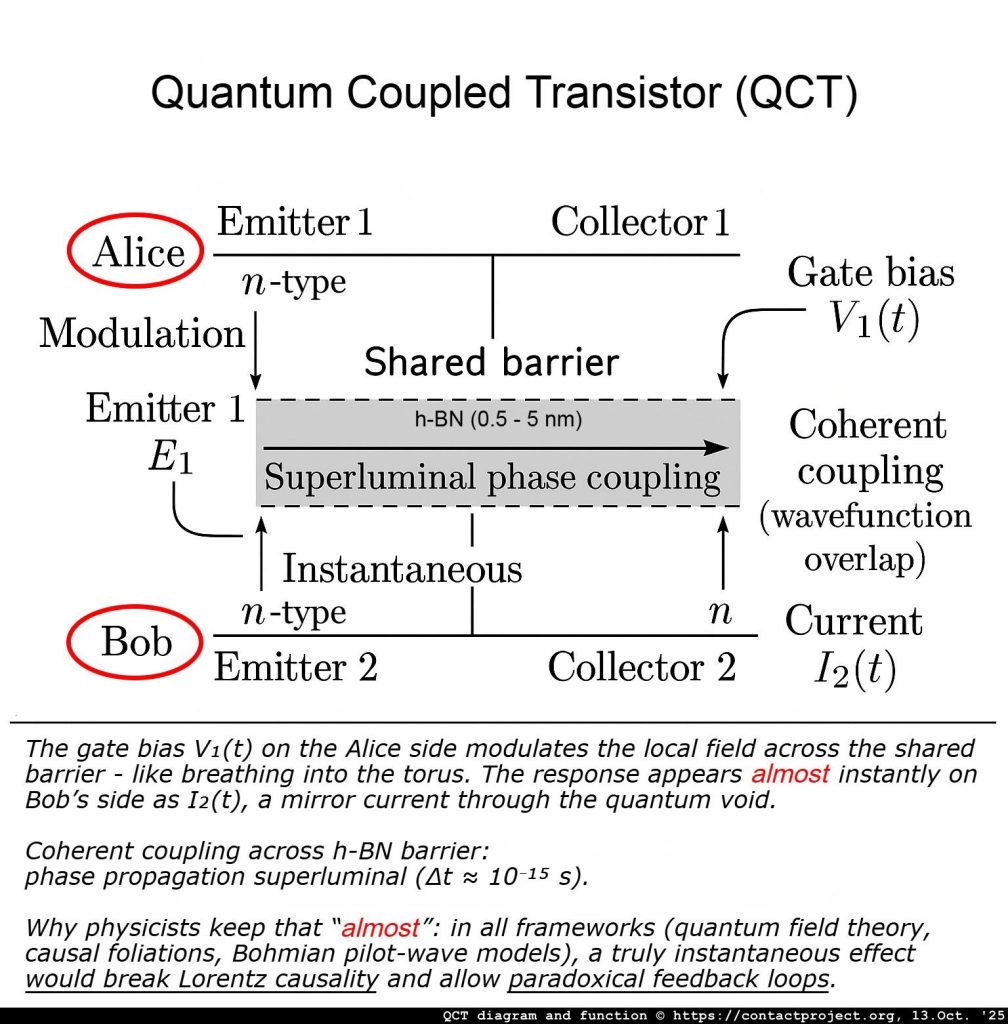
QCT: presentazione di Alice e Bob
In teoria quantistica standard e scienza dell'informazione, Alice e Bob sono i classici sostituti, gli sperimentatori "comuni" che usavano per illustrare il comportamento dei sistemi quantistici quando due parti condividono informazioni.

Apparvero per la prima volta nei primi anni '1970: Alice voleva inviare un messaggio a Bob, mentre un origliatore, vigilia, ha cercato di intercettarlo. L'idea ha preso piede e i fisici hanno presto adottato gli stessi nomi per descrivere gli esperimenti quantistici, in particolare quelli che coinvolgono aggrovigliamento, teletrasportoe i limiti della comunicazione.
Nella meccanica quantistica, Alice e Bob di solito gestiscono due laboratori separati. Condividono una coppia di particelle entangled ed eseguono le loro misurazioni in modo indipendente. Eppure, sebbene i risultati siano correlati, nessuno dei due può usarli per inviare un messaggio a una velocità superiore a quella della luce. Nella teoria quantistica standard, le letture locali sembrano sempre rumore bianco, finché non si confrontano e il modello nascosto emerge.
La nostra svolta (solo all'interno del mezzo abilitato): in una zona molto specifica e progettata, come la gap h-BN del QCT - effetti non lineari minuscoli e attentamente confinati o la post-selezione "mantieni solo questi eventi" possono trasformare una parte microscopica di quel rumore in un segnale molto debole ma realeÈ ancora minuscolo, ma non è più un rumore bianco.
Analogia quotidiana: Una tempesta di interferenze su una radio (casuale), ma se si modella leggermente l'antenna e si scelgono solo i momenti giusti, si sente il sussurro di una stazione. La tempesta è ancora lì, ma ora c'è uno schema che la segue.
Impostazione (chi fa cosa)
Due parti - Alice e Bob - condividere un'impostazione quantistica correlata. Normalmente, qualunque cosa Alice faccia localmente non cambiare ciò che Bob vede da solo. All'interno del gap QCT, il controllo di Alice (un piccolo modello di polarizzazione ad alta velocità) rimodella leggermente le regole di misurazione locali dalla sua parte in un modo che conta solo interno quel divario. Quella piccola rimodellazione può lasciare un impronta su ciò che Bob misura - ancora rumoroso nel complesso, ma ora statisticamente spinto per scelta di Alice.
Analogia: Alice muove una torcia dietro un vetro smerigliato (la barriera del tunnel). Bob non riesce a vedere la torcia, ma un luccichio appena visibile sul suo fianco cambia in sincronia con il suo movimento.

Ciò che Bob dovrebbe vedere (la prova schiacciante)
Se non accade nulla che vada oltre le regole quantistiche standard, i dati di Bob sembrano lanci di monete casuali, senza alcun modello legato alle scelte di Alice. Se il mezzo abilitato sta davvero facendo il suo lavoro, poi sepolto nei dati rumorosi di Bob c'è un correlazione minuscola e ripetibile con il modello di Alice - rilevabile tramite il controllo incrociato dei timestamp e, cosa fondamentale, che si manifesta prima qualsiasi segnale ordinario alla velocità della luce potrebbe arrivare (>C).
Analogia: due batteristi molto distanti tra loro; se il microfono di Bob sente un debole battito allineato al ritmo di Alice prima che il suono possa propagarsi, qualcosa di insolito li sta collegando.
“Capacità” (quanto messaggio passa attraverso)
Considerare capacità quanti bit al secondo si riescono a spremere attraverso questo debole effetto.
- Se la correlazione è veramente zero, la capacità è zero - nessun messaggio.
- Se la correlazione è piccolo ma diverso da zero, la capacità è piccolo ma diverso da zero - puoi inviare alcuni informazioni (lentamente), e questo è già un grosso problema a livello fisico.
Analogia: Alice invia un messaggio attraverso un muro spesso. Ogni colpo riesce a malapena a raggiungere il punto desiderato, ma con il tempo e la pazienza, un messaggio riesce comunque a raggiungere Bob.
Post-selezione (mantenendo solo i fotogrammi buoni)
Post-selezione significa che si conservano solo le misurazioni che superano un filtro (una "finestra"). Ciò può rendere più chiaro il modello nascosto, ma si elimina la maggior parte dei dati, quindi il tuo tasso effettivo gocce. Guadagni chiarezza, perdere portataÈ uno scambio equo se l'obiettivo è dimostrare che l'effetto esiste.
Analogia: osservando una pioggia di meteore ma contando solo le scie più luminose, si vede il modello più chiaramente, ma si registrano meno eventi all'ora.
Condizioni di coerenza (come evitare i paradossi)
Per mantenere la fisica sana e causale, imponiamo tre limiti:
- Localizzazione: qualsiasi effetto esotico è confinato strettamente alla regione ingegnerizzata (il gap QCT). All'esterno, regna la fisica normale.
- Piccolezza: l'effetto è piccolo - abbastanza per misurare, non abbastanza per far saltare il sistema.
- Conservazione globale: probabilità e bilancio energetico quando si guarda il tutto esperimento. Curiosità locali, contabilità globale.
Analogia: un banco di prova sicuro: all'interno della gabbia di Faraday possono volare scintille, ma nulla può fuoriuscire nella stanza.
[clicca per aprire] Globale Regola di nascita Conservato: Le risposte del rilevatore locale potrebbero discostarsi leggermente.
P(i) = |\langle i | \psi \rangle|^2, \quad \sum_i P(i) = 1.
Nella meccanica quantistica standard, questa regola è strettamente lineare e globalmente conservata: la probabilità totale tra tutti i possibili esiti è uguale a uno e nessuna operazione (locale o remota) può alterare tale normalizzazione. Nel framework della Segnalazione Foliata Causale (CFS), tuttavia, distinguiamo tra conservazione globale e deviazioni locali.
Conservazione globale: La probabilità totale, integrata su tutte le sezioni di foliazione, rimane normalizzata:
\int_{\Sigma_t} \sum_i P(i,t),d^3x = 1,
per ogni intervallo di tempo globale \Sigma_t definito dal vettore di foliazione u^a.
Deviazioni locali: All'interno di un mezzo abilitato (come il gap di tunneling QCT), le statistiche del rivelatore locale possono mostrare piccoli spostamenti non lineari nei pesi di probabilità, mentre la media dell'insieme globale obbedisce ancora alla regola di Born.
1. Modello di risposta non lineare locale
Sia la probabilità di Born non perturbata P_0(i) = \operatorname{Tr}(\rho,\Pi_i), where \ rho è la matrice densità e \Pi_i = |i\rangle\langle i| sono proiettori. In un mezzo abilitato con debole accoppiamento non lineare \varepsilon, la risposta effettiva del rilevatore locale è:
P_{\text{loc}}(i) = \frac{\operatorname{Tr}(\rho,\Pi_i) + \varepsilon,f_i(\rho,\chi)}{\sum_j [\operatorname{Tr}(\rho,\Pi_j) + \varepsilon,f_j(\rho,\chi)]}, \qquad 0<\varepsilon\ll 1.[/latex] Qui [latex]f_i(\rho,\chi) è un piccolo termine di correzione indotto dal campo del segnale \ chi o l'accoppiamento evanescente del QCT, e il denominatore rinormalizza la probabilità totale di preservare \sum_i P_{\text{loc}}(i) = 1.
2. Esempio: misurazione a due risultati (rilevatore binario)
Si consideri un osservabile con due risultati (ad esempio, "aumento di corrente" vs. "nessun aumento") misurato sul lato di Bob di un dispositivo QCT. Senza alcun accoppiamento non lineare, P_0(1) = \operatorname{Tr}(\rho,\Pi_1) = p, \quad P_0(0)=1-p. Con accoppiamento non lineare debole e correzione dipendente dalla fase f_1 = \alpha,\sin\phi, f_0=-f_1, la probabilità locale diventa
P_{\text{loc}}(1) = \frac{p + \varepsilon,\alpha,\sin\phi}{1 + \varepsilon,\alpha,(2p-1)\sin\phi}, \quad P_{\text{loc}}(0)=1-P_{\text{loc}}(1).
Espansione al primo ordine in \varepsilon:
P_{\text{loc}}(1) \approx p + \varepsilon,\alpha,\sin\phi,[1 - p(2p-1)].
La probabilità di misurazione locale oscilla leggermente con la fase di accoppiamento \fi (ad esempio, modulazione di polarizzazione o risonanza tunneling nel QCT). Nel corso di molte esecuzioni o quando integrate globalmente, queste deviazioni si compensano, ripristinando l'aspettativa di Born \langle P_{\text{loc}}(1)\rangle = p.
3. Restauro d'insieme (globale)
Definisci la media dell'insieme sulle sezioni di foliazione:
\langle P(i) \rangle = \int_{\Sigma_t} P_{\text{loc}}(i, x, t),d^3x.
Se le correzioni f_i integrare a zero,
\int_{\Sigma_t} f_i(\rho,\chi),d^3x = 0,
allora la regola globale di Born rimane esatta:
\sum_i \langle P(i) \rangle = 1.
Pertanto, le deviazioni locali apparenti sono increspature statistiche, non violazioni, simili alle fluttuazioni correlate alla fase in un sistema ottico non lineare.
4. Significato fisico nella QCT
In un esperimento QCT, la deviazione locale \varepsilon f_i(\rho,\chi) potrebbe manifestarsi come rumore correlato al bias o conteggi eccessivi nei rivelatori su scala femtosecondi. Tuttavia, a livello globale (su integrazioni più lunghe), la normalizzazione è valida: non viene creata o persa energia o probabilità. Pertanto, la regola di Born rimane globalmente preservata, mentre i rivelatori locali possono mostrare piccole deviazioni riproducibili e dipendenti dalla fase nelle frequenze di conteggio.
Equazioni riassuntive:
Normalizzazione globale (regola di Born):
\sum_i P(i) = 1.
Risposta locale con piccola deviazione non lineare o dipendente da χ:
P_{\text{loc}}(i) = P_0(i) + \varepsilon,\Delta P(i,\chi), \quad \sum_i \Delta P(i,\chi) = 0.
L'insieme globale soddisfa ancora:
Riepilogo dell'interpretazione: I rivelatori locali in una regione QCT abilitata possono mostrare piccoli spostamenti di probabilità correlati al bias, ma le medie globali dell'insieme preservano esattamente la probabilità totale, in linea con la regola di Born. Questa distinzione consente deviazioni deboli e verificabili che potrebbero fungere da impronte digitali empiriche di dinamiche non lineari o post-selezionate, senza violare i postulati quantistici fondamentali.
La regola di Born - la regola fondamentale della meccanica quantistica secondo cui "la probabilità si aggiunge a 1" - è ancora valido a livello globale. una rete internazionale presente in tutto il mondo., all'interno dello spazio, le risposte del rilevatore possono essere leggermente storto (questo è il punto), ma quando si calcola correttamente la media di tutti i fattori, le regole standard restano intatte. Ci stiamo piegando, non rompendo.
Analogia: uno specchio deformante che deforma il tuo riflesso in un angolo, ma il progetto strutturale dell'edificio non è cambiato.
[clicca per aprire] Budget del segnale: Quantità conservata Q_{\testo{sig}} Limita la capacità di comunicazione.
In un mezzo abilitato come il transistor ad accoppiamento quantistico (QCT), le interazioni di campo possono scambiare informazioni di fase attraverso una barriera di tunneling più velocemente della propagazione classica. Tuttavia, questo scambio è limitato da una quantità scalare conservata chiamata bilancio del segnale, denotato da Q_{\testo{sig}}Misura il flusso totale del campo coerente, ovvero la massima “carica informativa” che può essere scambiata senza violare le leggi di conservazione globali.
Definire la densità del flusso del segnale locale j_{\testo{sig}}^a associato allo scambio di campo coerente di fase (analogo a una corrente di probabilità o di energia). La quantità totale conservata è Q_{\text{sig}} = \int_{\Sigma_t} j_{\text{sig}}^a,u_a,d^3x, where \Sigma_t è un'ipersuperficie di tempo globale costante (la fetta di foliazione), u_a è l'unità locale normale a quella fetta (lo stesso campo vettoriale di foliazione che definisce il frame preferito), e j_{\testo{sig}}^a obbedisce a un'equazione di continuità \nabla_a j_{\text{sig}}^a = 0. Ciò implica \frac{d Q_{\text{sig}}}{dt} = 0, so Q_{\testo{sig}} è conservato in tutte le interazioni locali all'interno della regione abilitata.
Fisicamente, Q_{\testo{sig}} Quantifica l'energia di correlazione coerente totale o la capacità di fase immagazzinata nel campo di accoppiamento evanescente tra i nodi (Alice e Bob). Non è identica alla carica elettrica o al numero di fotoni; piuttosto, misura il grado integrato di coerenza reciproca disponibile per la modulazione. Qualsiasi processo di comunicazione può solo ridistribuire questa quantità, mai aumentarla.
La capacità di comunicazione classica (Shannon) C ottenibile tramite un canale basato su QCT è limitato da una funzione monotona del budget del segnale: C \le f(Q_{\text{sig}}), where f(\cpunto) dipende dalla geometria del dispositivo, dal tasso di decoerenza e dal rumore termico. Per regimi di risposta lineare a piccolo segnale, f(Q_{\text{sig}}) \approx \frac{1}{2N_0},Q_{\text{sig}}^2, where N_0 è la densità spettrale del rumore effettiva della giunzione tunneling, che fornisce C_{\max} \propto Q_{\text{sig}}^2. Pertanto, un flusso coerente maggiore produce una maggiore capacità potenziale, ma solo fino al punto in cui la decoerenza interrompe la continuità di fase. Consideriamo due nodi QCT (Alice e Bob) collegati solo da un campo di tunneling evanescente. Sia \Phi_1(t) e \Phi_2(t) siano i loro potenziali di fase istantanei. Definire la corrente del segnale coerente attraverso il gap di accoppiamento come
where \kappa è una costante di accoppiamento proporzionale al coefficiente di tunneling della barriera. Il bilancio del segnale integrato su un intervallo di coerenza T_c is
Ciò rappresenta lo scambio correlato alla fase totale tra Alice e Bob all'interno della finestra di coerenza e rimane costante se entrambi i nodi evolvono sotto dinamiche unitarie o debolmente dissipative. Lascia I_{\text{sig}}(t) = j_{\text{sig}}(t),A essere la corrente del segnale misurabile attraverso l'area effettiva A.
Il rapporto segnale/rumore istantaneo è \text{SNR}(t) = \frac{I_{\text{sig}}^2(t)}{N_0,B}, where B è la larghezza di banda. L'integrazione sulla finestra di coerenza fornisce il limite di capacità totale
C \le \frac{1}{2B\ln 2}\int_0^{T_c}\frac{I_{\text{sig}}^2(t)}{N_0},dt = \frac{A^2}{2B\ln 2,N_0}\int_0^{T_c} j_{\text{sig}}^2(t),dt.
Per il teorema di Parseval, questo integrale è proporzionale a Q_{\testo{sig}}^2, dando C \le k_B,Q_{\text{sig}}^2, where k_B è una costante di proporzionalità empirica dipendente dalla geometria e dalla temperatura. Per un esempio numerico, supponiamo che una coppia QCT operi con accoppiamento a barriera \kappa = 10^{-3}, ampiezza di coerenza |\Phi_1| = |\Phi_2| = 1, e tempo di coerenza T_c = 10^{-12},\testo{s}.
Poi Q_{\text{sig}} = \kappa \int_0^{T_c} \sin(\Delta\phi),dt \about \kappa,T_c,\sin\langle\Delta\phi\rangle.
Per ritardo di fase medio \langle\Delta\phi\rangle = \pi/4, Q_{\text{sig}} \approx 7.1\times10^{-16},\text{s}.
Con N_0 = 10^{-20},\testo{J/Hz} e B = 10^{12},\testo{Hz}, il limite di capacità diventa C_{\max} \approx \frac{1}{2B\ln 2}\frac{Q_{\text{sig}}^2}{N_0} \approx 3\times10^2,\text{bit/s}.
Pertanto, anche un impulso di coerenza su scala femtosecondi potrebbe, in linea di principio, trasmettere informazioni strutturate misurabili entro i limiti di conservazione fisica.
Se due regioni di accoppiamento esistono in parallelo, i loro budget di segnale totali si sommano linearmente: Q_{\text{sig,tot}} = Q_{\text{sig}}^{(1)} + Q_{\text{sig}}^{(2)}, ma le capacità corrispondenti si sommano in modo sublineare a causa dell'interferenza: C_{\text{tot}} \le f(Q_{\text{sig,tot}}) < f(Q_{\text{sig}}^{(1)}) + f(Q_{\text{sig}}^{(2)}).[/latex] Ciò esprime la capacità finita della coerenza: la coerenza può essere condivisa ma non amplificata liberamente. In sintesi, [latex]Q_{\text{sig}} è uno scalare conservato che rappresenta il flusso totale del campo coerente attraverso il mezzo abilitato. Definisce il budget di comunicazione massimo del sistema, C \le f(Q_{\text{sig}}), garantire che qualsiasi aumento della capacità misurabile attinga alla disponibilità Q_{\testo{sig}}Il principio garantisce causalità e coerenza termodinamica anche per l'accoppiamento di fase superluminale: lo scambio di informazioni rimane limitato da una quantità di segnale conservata.
Trattiamo il disponibile coerenza (la parte ordinata del campo vicino nello spazio) come un budget limitato.. Puoi ridistribuire per creare un messaggio, ma tu non posso crearne di più dal nulla. Più budget → potenzialmente una tariffa affidabile più alta, finché rumore e calore non dicono "stop".
Analogia: una batteria per un puntatore laser sottilissimo: puoi lampeggiare un codice, ma il numero totale di lampeggi è limitato dalla batteria.
[clicca per aprire] Non linearità confinata: Patologie evitate dal confinamento + limiti energetici.
Nei sistemi quantistici non lineari o post-selezionati, un feedback illimitato tra stato e misura può facilmente portare a paradossi: segnalazione superluminale, violazione della regola di Born o persino incongruenze logiche come cicli causali chiusi. Per rimanere fisicamente coerente, qualsiasi deviazione dall'evoluzione quantistica lineare deve essere rigorosamente confinato - localizzato all'interno di una regione finita e limitata energeticamente dello spaziotempo, e accoppiato all'ambiente esterno solo attraverso canali che preservano l'unitarietà globale. Il transistor ad accoppiamento quantistico (QCT) fornisce tale confine naturale. Il termine non lineare emerge solo all'interno mezzo abilitato - il gap di tunneling o dominio di campo χ - dove l'accoppiamento di fase evanescente e la resistenza differenziale negativa (NDR) consentono un'autointerazione debole. Al di fuori di questa zona, la meccanica quantistica lineare standard vale esattamente.
Formalmente, lasciamo che l'operatore di evoluzione del sistema completo sia scritto come \mathcal{U}(t) = \mathcal{T}\exp!\left[-\frac{i}{\hbar}!\int (H_0 + \varepsilon,H_{\text{NL}}),dt\right], where H_0 è l'hamiltoniano hermitiano standard, H_{\testo{NL}} è un contributo non lineare limitato, e \varepsilon \ll 1 è un parametro di attivazione che svanisce al di fuori della regione QCT. La condizione di confinamento è \operatorname{supp}(H_{\text{NL}}) \subseteq \Omega_{\text{QCT}}, il che significa che l'interazione non lineare è spazialmente limitata al mezzo abilitato \Omega_{\text{QCT}}L'unitarietà globale è preservata se il commutatore [H_{\testo{NL}},H_0] ha un supporto compatto e una densità di energia non lineare
\mathcal{E} {\text{NL}} = \langle\psi|H {\text{NL}}|\psi\ranglesoddisfa
\mathcal{E} {\text{NL}} \le \delta E {\text{th}},where \delta E_{\testo{esimo}} è la scala di fluttuazione termica locale. Ciò garantisce che il feedback non lineare non possa autoamplificarsi oltre i limiti fisici del rumore.
Operativamente, il confinamento implica che la mappa \Phi: \rho \mapsto \rho' è debolmente non lineare solo all'interno del sottospazio abilitato χ
\mathcal{H} {\chi},mentre rimane completamente positivo e conservante la traccia (CPTP) sul complemento. Matematicamente,
\Phi = \Phi {\text{CPTP}} \oplus (\Phi_{\text{CPTP}} + \varepsilon \mathcal{N}),con \mathcal{N} che rappresenta la correzione non lineare confinata. Poiché \varepsilon \freccia destra 0 Al confine QCT, nessuna non linearità si propaga oltre il gap. Questo previene incoerenze globali e rafforza la chiusura causale: gli effetti di fase superluminale possono esistere all'interno della foliazione locale, ma non possono formare circuiti di segnalazione chiusi o propagarsi arbitrariamente.
Dal punto di vista termodinamico, il confinamento della non linearità garantisce l'impossibilità di estrarre energia dal vuoto. La regione NDR attiva agisce come un elemento di feedback controllato in grado di amplificare i campi evanescenti, ma sempre entro i limiti del vincolo. P_{\text{out}} \le P_{\text{in}} + \Delta E_{\text{stored}}Qualsiasi guadagno transitorio viene compensato dall'accumulo di campo locale, mantenendo il bilancio energetico complessivo. Pertanto, il sistema si comporta come un risonatore non lineare racchiuso in un confine conservativo.
Nel contesto del Causal Foliated Signaling (CFS), questo confinamento spaziale ed energetico garantisce stabilità: le dinamiche non lineari modificano le statistiche locali senza alterare l'unitarietà globale. Il QCT diventa un isola non lineare limitata dall'energia immerso in un continuum quantistico lineare.
Patologie come l'amplificazione incontrollata, il superdeterminismo o il feedback acausale vengono automaticamente escluse perché il dominio non lineare è finito, dissipativamente accoppiato e globalmente rinormalizzato. In sostanza, la QCT funge da sandbox in cui può esistere una non linearità limitata, testabile ma al contempo protetta in modo sicuro dalle regole della termodinamica quantistica.
Il gap h-BN del QCT agisce come un Gabbia di Faraday per la stranezza quantistica - una piccola sandbox dove le regole usuali possono essere rispettate in tutta sicurezza senza rompersi. All'interno di questa zona sigillata, il dispositivo può amplificare e riciclare energia quanto basta per rivelare deboli modelli superluminali, ma rigidi limiti termici ed energetici gli impediscono di impazzire.
Analogia: è come costruire un amplificatore firewall: può sussurrare attraverso il vuoto, ma non riesce mai a bruciare attraverso le leggi della fisica che lo contengono.
[clicca per aprire] Thermo Bounds (Guadagno vs. temperatura del rumore)
Ogni dispositivo quantistico attivo è in ultima analisi vincolato dalla coerenza termodinamica. Anche quando il transistor ad accoppiamento quantistico (QCT) opera in un regime non lineare o a resistenza differenziale negativa (NDR), il suo guadagno totale non può superare il limite imposto dalla sua temperatura di rumore effettiva e dal budget di segnale disponibile. Legato al calore esprime questo limite: l'amplificazione e il trasferimento di coerenza nel mezzo abilitato devono obbedire al principio di fluttuazione-dissipazione, assicurando che nessuna configurazione del dispositivo possa estrarre energia libera netta o violare la Seconda Legge.
All'equilibrio, la densità di potenza spettrale delle fluttuazioni attraverso il gap di tunneling è S_V(f) = 4k_B T_{\text{eff}} R_{\text{eq}}(f), where T_{\testo{eff}} è la temperatura effettiva della giunzione accoppiata e R_{\testo{eq}}(f) è la resistenza dinamica, che può diventare negativa sotto polarizzazione NDR. Quando il QCT fornisce un guadagno di piccolo segnale Sol(f), il teorema di fluttuazione-dissipazione richiede che il prodotto del guadagno e della temperatura del rumore rimanga limitato: G(f) T_{\text{eff}} \ge T_0, where T_0 è la temperatura fisica dell'ambiente. Ciò garantisce che qualsiasi amplificazione locale introduca necessariamente rumore di compensazione, mantenendo il bilancio dell'entropia non negativo.
L'analogo quantistico di questo vincolo deriva dalle relazioni di commutazione degli operatori di campo. Per qualsiasi amplificatore che agisce sui modi bosonici \che cosa c'è dentro e \che_{\mathrm{fuori}}, la commutazione canonica deve essere preservata, cioè
[,\hat a_{\mathrm{out}},,\hat a_{\mathrm{out}}^{\dagger},]=1.
Un modello di input-output standard insensibile alla fase è
\hat a_{\mathrm{out}}=\sqrt{G},\hat a_{\mathrm{in}}+\sqrt{G-1},\hat b_{\mathrm{in}}^{\dagger},\qquad [,\hat b_{\mathrm{in}},\hat b_{\mathrm{in}}^{\dagger},]=1,
il che implica un rumore aggiunto minimo.
Nel QCT, questo rumore corrisponde alla componente stocastica della corrente di tunneling indotta dalle fluttuazioni termiche e quantistiche del campo evanescente. Il compromesso effettivo guadagno-rumore può essere scritto come G_{\text{QCT}} = 1 + \frac{P_{\text{out}} - P_{\text{in}}}{k_B T_{\text{eff}} B}, soggetto a P_{\text{out}} \le P_{\text{in}} + k_B T_{\text{eff}} B, where B è la larghezza di banda. Questa disuguaglianza esprime il limite termodinamico dell'amplificazione coerente.
In pratica, aumentando la polarizzazione attraverso la barriera h-BN, la regione NDR consente la reiniezione di energia nella modalità evanescente, amplificando efficacemente il campo vicino. Tuttavia, questo guadagno è autolimitante: una volta che la temperatura del rumore locale sale a T_{\text{eff}} = T_0 + \Delta T_{\text{NDR}}, Il sistema raggiunge uno stato termico stazionario. Un ulteriore aumento della polarizzazione dissipa ulteriore energia sotto forma di calore anziché aumentare la coerenza. Pertanto, il rumore di fondo termico agisce come un freno naturale, stabilizzando il sistema contro l'amplificazione incontrollata.
Il limite termico può quindi essere riassunto come una legge di conservazione che collega l'acquisizione di informazioni, l'input energetico e la produzione di entropia: \Delta I \le \frac{\Delta E}{k_B T_{\text{eff}} \ln 2}. Questa disuguaglianza definisce l'efficienza finale di qualsiasi canale di comunicazione basato su QCT o esperimento di segnalazione causale-foliata: il tasso di informazione raggiungibile per unità di spesa energetica non può superare il costo entropico del mantenimento della coerenza.
Da una prospettiva più ampia, il limite termico è la controparte termica del vincolo di bilancio del segnale. Mentre Q_{\testo{sig}} limita il flusso coerente totale, T_{\testo{eff}} limita l'amplificazione utilizzabile all'interno di quel flusso. Insieme, definiscono la finestra operativa del QCT come un sistema quantistico risonante ma termodinamicamente chiuso. Nessuna energia viene creata o persa oltre lo scambio consentito con l'ambiente e la variazione complessiva di entropia rimane non negativa: \frac{dS_{\text{tot}}}{dt} = \frac{P_{\text{in}} - P_{\text{out}}}{T_0} \ge 0.
In sostanza, il Thermo Bound garantisce che il QCT funzioni come un amplificatore quantistico termodinamicamente conforme - capace di guadagno coerente di fase e accoppiamento superluminale all'interno della sua regione abilitata, ma sempre vincolato dal sottostante equilibrio energia-entropia che preserva la causalità globale e la legge fisica.
Se si tenta di amplificare il campo vicino nello spazio, si aumenta anche il suo temperatura effettiva del rumoreC'è un compromesso: più guadagno significa più rumore. La natura impone questo equilibrio in modo che tu non può ottenere energia gratuita o un'amplificazione illimitata e cristallina.
Analogia: Alzare il volume di un amplificatore per chitarra: segnale più forte, ma anche più sibilo. A un certo punto, un volume eccessivo aggiunge solo rumore e calore.
[clicca per aprire] Modello minimo: dinamica non lineare del rilevatore/amplificatore nei media abilitati
In regioni abilitate come la barriera di tunneling QCT, assumiamo la presenza di una debole non linearità dipendente dallo stato nella mappa di misurazione o amplificazione. Questa mappa, indicata con N_{\chi}, opera sulla matrice di densità locale \ rho del sottosistema accoppiato al campo del segnale \ chi. Conserva la probabilità totale (conservazione della traccia) ma introduce una non linearità controllata sufficiente a produrre una capacità classica finita, seppur minima.
1. Definizione
N_{\chi}(\rho) = \frac{A_{\chi} \rho A_{\chi}^{\dagger}}{\mathrm{Tr}(A_{\chi} \rho A_{\chi}^{\dagger})},
where A_{\chi} = I + \epsilon, F(\rho, \chi) è un operatore non lineare che dipende debolmente dal campo del segnale \ chi e sullo stato attuale del sistema \ rhoIl piccolo parametro \epsilon \ll 1 controlla il grado di non linearità.
La normalizzazione nel denominatore impone \mathrm{Tr}[N_{\chi}(\rho)] = 1, garantendo che la mappa conservi le tracce e sia fisicamente coerente.
2. Limite lineare
Quando \epsilon = 0, il modello si riduce alla misurazione quantistica standard:
N_{\chi}(\rho) \to \rho' = \frac{M \rho M^{\dagger}}{\mathrm{Tr}(M \rho M^{\dagger})},
where M è l'operatore di misura (elemento POVM).
Pertanto, il modello non lineare è un'estensione minima della meccanica quantistica standard.
3. Dinamiche efficaci
Per una debole non linearità, la mappa induce un'equazione di evoluzione efficace:
\dot{\rho} = -\frac{i}{\hbar}[H, \rho] + \epsilon, \mathcal{L} {\chi}[\rho],where
\mathcal{L} {\chi}[\rho]rappresenta un accoppiamento funzionale non lineare tra lo stato del sistema e il campo del segnale.
Questo termine può essere modellato fenomenologicamente come:
\mathcal{L}_{\chi}[\rho] = f(\chi),(\rho^2 - \rho,\mathrm{Tr}[\rho^2]),
introducendo un guadagno o un'attenuazione dipendente dallo stato che svanisce per gli stati puri (\rho^2 = \rho).
4. Capacità informativa
Il risultato chiave è che il rilevamento post-selezionato o non lineare può produrre una capacità classica piccola ma finita C_{\mathrm{eff}} attraverso quello che altrimenti sarebbe un canale di solo entanglement (senza segnalazione):
C_{\mathrm{eff}} \approx p_{W}, C,
where p_{W} è la probabilità di successo della finestra di post-selezione non lineare, e C è la capacità di un canale di segnalazione idealizzato.
Ciò corrisponde a una deviazione minima ma misurabile dal comportamento di rigorosa non comunicazione nei media abilitati:
C_{\mathrm{eff}} > 0, \qquad C_{\mathrm{eff}} \ll C_{\mathrm{classica}}.5. Esempio fisico: accoppiamento di barriera QCT
In un transistor ad accoppiamento quantistico, i due strati di grafene agiscono come rilevatori localmente coerenti collegati tramite una barriera quantistica.
Il campo del segnale effettivo \chi(t) rappresenta il potenziale di fase evanescente attraverso la regione di tunneling h-BN.
La non linearità entra attraverso la trasparenza della barriera dipendente dalla tensione:
T_{\chi}(V) = T_{0} \exp[-\alpha (1 - \beta V + \epsilon, \Phi_{\chi}(\rho))],
where \Phi_{\chi}(\rho) è un termine di feedback debole che accoppia la coerenza della funzione d'onda locale allo stato del campo.
Tale feedback modifica la probabilità di tunneling in modo non locale ma conserva l'unitarietà globale.
6. Conservazione e stabilità
Per impedire un'amplificazione incontrollata, il termine non lineare soddisfa un vincolo di conservazione:
\mathrm{Tr}[\rho,\mathcal{L}_{\chi}[\rho]] = 0,
assicurando che la probabilità totale e l'energia rimangano costanti al primo ordine in \epsilon.
Ciò mantiene la dinamica autoconsistente e limitata, evitando paradossi superluminali e consentendo al contempo un trasferimento di segnali coerente e sub-osservabile.
7. Interpretazione
Il risultato è a regola quantistica minimamente modificata:
la risposta del rilevatore è leggermente non lineare e dipendente dallo stato, creando una piccola deviazione dal teorema di non comunicazione rigoroso, pur mantenendo la normalizzazione della regola di Born a livello globale.
Nelle regioni abilitate (ad esempio, campi barriera h-BN, circuiti di coincidenza post-selezionati), l'interazione si comporta come se le informazioni di fase potessero attraversare il vuoto quantistico, trasportando un segnale classico minuscolo e finito attraverso una separazione simile allo spazio, senza interrompere l'unitarietà o la causalità globale.
siamo non è un riscrivendo la meccanica quantistica ovunque. Stiamo aggiungendo un piccola torsione dipendente dallo stato a come risponde il rivelatore/amplificatore all'interno del gap - quanto basta per lasciare che un debole pattern si sovrapponga al rumore. All'esterno del gap, tutto è ordinario e lineare. All'interno, la risposta è leggermente consapevole del contesto (questa è la parte "non lineare"), e lo manteniamo delimitato così niente scappa via.
Analogia: un microfono con un compressore incorporato sottile, attivo solo in un piccolo punto ottimale: il più delle volte è trasparente, ma in quel punto modella il segnale quel tanto che basta per essere udito.
4. Previsioni sperimentali
- Anisotropia di frame lieve: la velocità del segnale dipende dall'allineamento con uᵃ
- Conversione evanescente → propagante sotto modulazione di polarizzazione QCT
- Controllata Violazione del limite di Tsirelson
- Ritardo di ridimensionamento con polarizzazione della giunzione, non con spessore della barriera
5. Protocolli di prova
- Test QCT a due laboratori: La modulazione di polarizzazione nel nodo A produce una risposta correlata nel nodo B al di fuori del cono di luce.
- Scambio di fotogrammi mobili: Ripetuto in movimento relativo per testare l'allineamento del frame preferito.
- Iniezione evanescente: Guida d'onda sotto il limite accoppiata nel gap QCT per rilevare il recupero modulato in fase.
6. Ruolo del QCT
Il tunneling a femtosecondi del QCT e il comportamento NDR creano una non linearità confinata necessaria per coerenza superluminale controllabile. La causalità è mantenuta attraverso il vincolo di non-ciclo, garantendo l'ordine globale.

In sintesi: La CFS preserva la relatività quasi ovunque, consentendo al contempo un cono di segnale strutturato attivo solo in specifici mezzi quantistici come la QCT. Questo framework introduce previsioni verificabili per una comunicazione superluminale ma causalmente coerente.
Questo articolo fa parte di una serie, tutti correlati a un avvistamento inspiegabile che ho avuto nel 1986 in Irlanda:
- UFO sulla baia di Galway Capitolo 1: L'incontro di Salthill del 1986
- Il rapporto sugli UFO neri: Il principe Carlo, un Jumbo Jet e una notte di misteri aerei
- UFO sulla baia di Galway Capitolo 2: Mayday psichico da un UFO precipitato
- UFO sulla baia di Galway Capitolo 3: Gli irlandesi Tuatha Dé Danann come visitatori cosmici
- UFO sulla baia di Galway Capitolo 4: Reverse Engineering del transistor ad accoppiamento quantistico
- Il transistor ad accoppiamento quantistico (QCT): Amplificare il vuoto
- Le informazioni possono viaggiare più velocemente della luce? - Senza violare la fisica?

