🕔 अनुमानित पढ़ने का समय: 32 मिनट
कारण-पर्णित संकेतन का तर्क
का सिद्धांत कारण-पर्णित संकेतन (सीएफएस) प्रस्तावित करता है कि समय में छिपी हुई परतें होती हैं जो क्वांटम प्रणालियों के बीच सीमित प्रकाश-से-तेज़ सुसंगतता को संभव बनाती हैं। शोधकर्ता जल्द ही इसका उपयोग कर सकते हैं क्वांटम-युग्मित ट्रांजिस्टर (QCT) - एक दोहरे ग्राफीन नैनोडिवाइस - इन प्रभावों का प्रत्यक्ष परीक्षण करने और यह निर्धारित करने के लिए कि क्या वे भौतिकी के ज्ञात नियमों को तोड़े बिना घटित हो सकते हैं।
अपने मूल में, सीएफएस एक उत्तेजक प्रश्न पूछता है: क्या होगा यदि कुछ प्रकार की तरंगें, जैसे कि क्षणभंगुर या निकट क्षेत्र तरंगें, प्रकाश की तुलना में अधिक तेजी से कला संबंधी जानकारी साझा कर सकें, फिर भी कार्य-कारण संबंध को बनाए रखें?
अगर ऐसा है, तो स्पेसटाइम पूरी तरह एकसमान नहीं हो सकता। इसमें एक सूक्ष्म आंतरिक संरचना हो सकती है - समय की एक "परत", जहाँ सूचना प्रत्येक परत के भीतर थोड़ा आगे बढ़ती है, जबकि समग्र रूप से एकरूप रहती है।

इस दृष्टिकोण में, ब्रह्मांड एक विशाल ब्रह्मांडीय पुस्तक के पन्नों की तरह खुलता है: प्रत्येक पृष्ठ एकदम सही क्रम में घूमता है, भले ही कुछ पृष्ठ दूसरों की तुलना में थोड़े तेज़ घूमते हों। सीएफएस सापेक्षता का एक परिष्कृत दृष्टिकोण प्रस्तुत करता है - एक ऐसा दृष्टिकोण जो कारण और प्रभाव की कहानी को अक्षुण्ण रखते हुए संरचित अतिप्रकाशीय सुसंगति की अनुमति देता है।
भाग II. कारण-पर्णित संकेतन (सीएफएस)
- मूल स्वयंसिद्ध
- गतिकी और गतिकी
- क्वांटम नियम और संरक्षण
- प्रायोगिक भविष्यवाणियाँ
- परीक्षण प्रोटोकॉल
- क्यूसीटी की भूमिका
1. मूल स्वयंसिद्ध
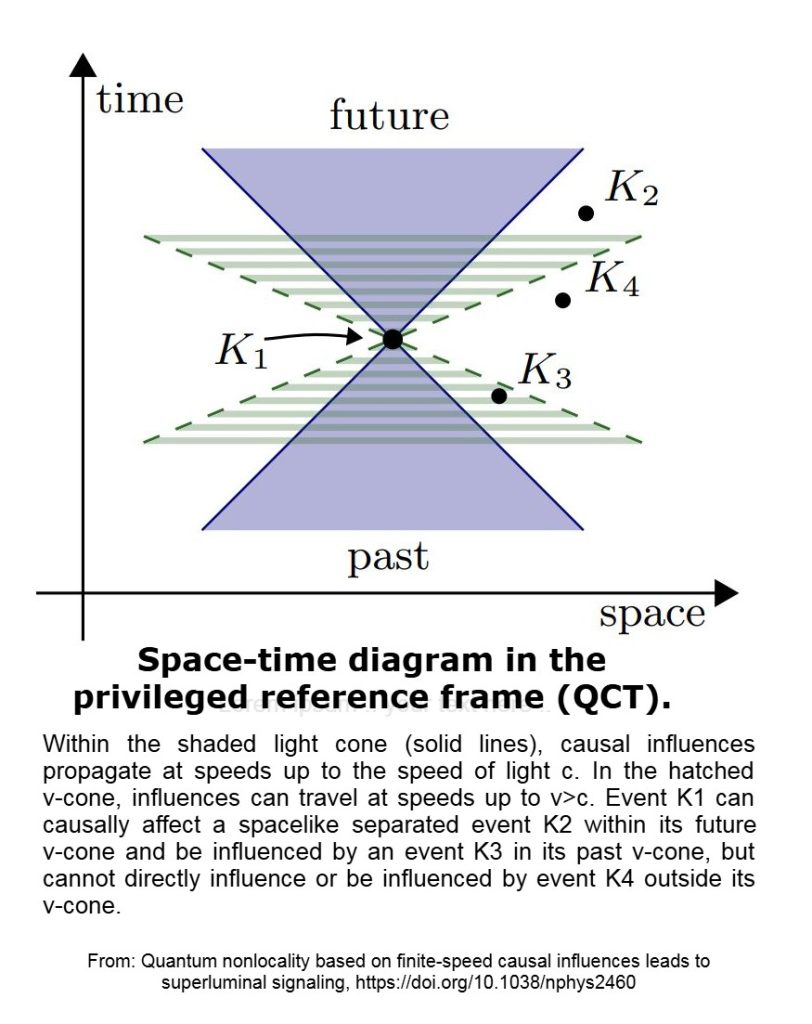
- वैश्विक समय पर्णन: स्पेसटाइम में एक पसंदीदा वैश्विक स्लाइसिंग (ब्रह्मांडीय समय, टाइमलाइक वेक्टर द्वारा परिभाषित) होती है उᵃ)। सभी संकेत - ल्यूमिनल और सुपरल्यूमिनल - इस पर्णन द्वारा क्रमबद्ध होते हैं।
- बड़ा सिग्नल शंकु: प्रकाश शंकु से परे, विशिष्ट मीडिया या क्षेत्रों (χ) के लिए एक व्यापक “सिग्नल शंकु” मौजूद है।
- कालक्रम संरक्षण: बंद सिग्नल लूप्स को सॉल्वेबिलिटी बाधाओं द्वारा गतिशील रूप से निषिद्ध किया जाता है।
- परिचालन स्थान: मानक प्रयोग लोरेन्ट्ज़-अपरिवर्तनीय रहते हैं; विचलन केवल सक्षम मीडिया के भीतर ही होता है।
2. गतिकी और गतिकी
- पसंदीदा फ़्रेम: सी.एम.बी. रेस्ट फ्रेम के साथ लगभग संरेखित।
- सिग्नल फ़ील्ड (χ): EM वाहकों से कमजोर रूप से जुड़ता है, जिससे कारणात्मक शंकु चौड़ा हो जाता है।
- सुपरल्यूमिनल विशेषताएँ: पीडीई सक्षम मीडिया में जी-लाइटकोन के बाहर प्रसार प्रदर्शित होता है।
- नो-लूप बाधा: अभिन्न स्थितियाँ समय-घटाने वाले कारणात्मक लूपों को रोकती हैं।
3. क्वांटम नियम और संरक्षण
हमने एक छोटा सा क्षेत्र (क्यूसीटी गैप) बनाया है, जहां क्वांटम निकट-क्षेत्रों को धीरे-धीरे आकार दिया जा सकता है, ताकि मुश्किल से पता लगाने योग्य, प्रकाश से तेज गति प्राप्त हो सके। पैटर्न अन्यथा यादृच्छिक डेटा में दिखाई देता है - भौतिकी को सुरक्षित रखने के लिए पर्याप्त छोटा, प्रयोगशाला में परीक्षण करने के लिए पर्याप्त स्पष्ट।

यदि उपरोक्त संक्षिप्त कथन आपके लिए अर्थपूर्ण है, तो आप रेडलाइन का विस्तार कर सकते हैं क्वांटम नियम अधिक विस्तृत चर्चा के लिए नीचे काले ▶ त्रिकोण पर क्लिक करें।
सामान्य पाठकों के लिए, प्रत्येक खंड में एक संक्षिप्त व्याख्या (बिना गणित के) और उसके बाद एक सादृश्य दिया गया है। हालाँकि ज़्यादातर लोगों ने इसके बारे में कभी नहीं सुना होगा। असंचार प्रमेय (उलझन द्वारा प्रकाश से भी तेज संचार को रोकना), इसे इसके मौलिक महत्व के कारण यहां प्रमुखता से रखा गया है, और क्योंकि नियंत्रित विश्राम उस नियम का यहाँ इसका अन्वेषण किया गया है।
[खोलने के लिए क्लिक करें] शिथिल नो-कम्युनिकेशन प्रमेय: सक्षम मीडिया में, गैर-रैखिक/पोस्ट-चयनित गतिशीलता छोटी शास्त्रीय क्षमता > 0 की अनुमति देती है।
दावा (परिचालनात्मक):
एक में सक्षम माध्यम (उदाहरण के लिए, χ-सक्षम निकट-क्षेत्र के रूप में कार्य करने वाला एक QCT अंतराल), एक कमजोर, स्थानीयकृत अरैखिकता or स्पष्ट पोस्ट-चयन एक उत्पादन कर सकते हैं छोटी लेकिन सीमित शास्त्रीय क्षमता सी>0 वैश्विक एकता या बोर्न नियम का उल्लंघन किए बिना अंतरिक्ष-समान-पृथक पक्षों के बीच।
व्यवस्था
चलो ρAB ऐलिस और बॉब द्वारा साझा की गई एक द्विपक्षीय स्थिति हो। मानक क्वांटम यांत्रिकी में स्थानीय के साथ सीपीटीपी मानचित्र और नहीं चयन के बाद, बॉब की कम हुई अवस्था ऐलिस की पसंद से स्वतंत्र है:
ρB′=TrA[(ΦA⊗IB)(ρAB)]=ρB, (नो-सिग्नलिंग)
एक में सक्षम क्यूसीटी क्षेत्र, ऐलिस के नियंत्रित संचालन को एक मॉडल के रूप में प्रस्तुत करता है कमजोर रूप से अरैखिक किसी का विक्षोभ सीपीटीपी मानचित्र:
ΦA(V)(⋅)=ΛA(⋅)+ε\mathcal{N}_A^{(V)}[⋅], 0<ε≪1,[/latex] जहाँ [latex]V ऐलिस का नियंत्रण है (उदाहरण के लिए, इंटरलेयर पूर्वाग्रह), एलए सीपीटीपी है और \mathcal{N}_A^{(V)} एक सीमित अरेखीय कार्यात्मक है जो केवल के अंदर सक्रिय है χ-सक्षम माध्यम.बॉब की स्थिति बन जाती है
ρB′(V)=TrA[(ΦA(V)⊗IB)ρAB]=ρB(0)+εΔρB(V),साथ में
ΔρB(V)=TrA [(NA(V)⊗IB)ρAB].\Delta\rho_B(V)=\mathrm{Tr}_A\!\Big[\big(\mathcal{N}_A^{(V)}\otimes \mathbb{I}_B\big)\rho_{AB}\Big].ΔρB(V)=TrA[(NA(V)⊗IB)ρAB].
If \Delta\rho_B(V_0)\neq \Delta\rho_B(V_1), तो बॉब के परिणाम आँकड़े (थोड़े से) ऐलिस की पसंद पर निर्भर करते हैं V, शास्त्रीय संचार को क्रम में सक्षम बनाना \varepsilon.
POVM के लिए \{मेरा\} बॉब पर, पता लगाने की संभावनाएं हैं
P(y∣V)=Tr[MyρB′(V)]=P0(y)+εΔP(y∣V),ΔP(y∣V):=Tr[MyΔρB(V)].कमजोर सिग्नलिंग वाली क्षमता
ऐलिस को एक बाइनरी प्रतीक भेजने दें X\in\{0,1\} चुनने के द्वारा वी\इन\{वी_0,वी_1\}.बॉब मापता है Y\में\{0,1\}. परिभाषित करना
\डेल्टा := P(Y=1\mid V_1)-P(Y=1\mid V_0)=\varepsilon\,\Delta P + O(\varepsilon^2),आधारभूत त्रुटि संभावना के साथ पी:=पी(वाई=1∣V0).
बाइनरी-इनपुट, बाइनरी-आउटपुट चैनल के लिए लघु-संकेत सीमा ∣\डेल्टा|\ll 1, शैनन क्षमता द्विघात सन्निकटन को स्वीकार करता है
C \;\लगभग\; \frac{\delta^2}{2\ln 2}\,\frac{1}{p(1-p)} \;+\; O(\delta^4), \qquad C>0\ \text{iff}\ \delta\neq 0.
इस प्रकार कोई भी शून्येतर \डेल्टा (इसलिए कोई भी शून्येतर \varepsilon-आदेश पर निर्भरता V) उत्पन्न करता है परिमित सी>0.
चयन के बाद की भूमिका
यदि बॉब (या एक संयुक्त संयोग सर्किट) पोस्ट-सिलेक्ट्स परिणाम विंडो पर W सफलता की संभावना के साथ पीडब्लू, सशर्त राज्य है
\rho_{B\!\mid W}(V)\;=\;\frac{\Pi_W\,\rho_B'(V)\,\Pi_W}{\mathrm{Tr}\!\big[\Pi_W\,\rho_B'(V)\big]}, \qquad \Pi_W=\Pi_W^\dagger=\Pi_W^2.सामान्यीकरण के कारण \mathrm{Tr}[\Pi_W\rho_B'(V)], मानचित्रण \rho'_B \mapsto \rho_B^{\mid W} is अरेखीय, और वातानुकूलित आँकड़े एक प्राप्त कर सकते हैं V-निर्भरता तब भी जब असुविधाजनक बिना सिग्नलिंग वाली समानता लागू होती है। व्यवहार में, चयन-पश्चात उपयोगी दर को इस प्रकार मापता है pW:
C_{\mathrm{eff}} \approx p_W , C.संगति की शर्तें
वैश्विक विकृतियों से बचने के लिए:
- स्थानीयकरण: \mathcal{N}_A^{(V)} तक ही सीमित है χ-सक्षम क्षेत्र (जैसे, QCT अंतराल)।
- छोटापन: \varepsilon स्थिरता और ऊर्जा सीमा को बनाए रखने के लिए पर्याप्त रूप से छोटा है।
- वैश्विक एकता एवं बोर्न नियम: समूह गतिशीलता CPTP बनी रहती है; विचलन (यदि कोई हो) वातानुकूलित, स्थानीय डिटेक्टर मानचित्रों (चयन के बाद) या माध्यम के अंदर कमजोर-गैर-रेखीय क्षेत्र तक ही सीमित होते हैं।
संक्षिप्त वक्तव्य
\बॉक्स्ड{ \begin{aligned} &\Phi_A^{(V)}=\Lambda_A+\varepsilon\,\mathcal{N}_A^{(V)},\quad \varepsilon\ll 1,\\ &\rho_B'(V)=\rho_B^{(0)}+\varepsilon\,\Delta\rho_B(V),\quad \Delta\rho_B(V)=\mathrm{Tr}_A\!\big[(\mathcal{N}_A^{(V)}\!\otimes\!\mathbb{I})\,\rho_{AB}\big],\\ &\exists\,M:\ \delta=\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_1)\big]-\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_0)\big]\neq 0 \\ &\Rightarrow\ C \approx \dfrac{\delta^2}{2\ln 2\, p(1-p)} \;>\;0,\quad C_{\text{eff}}\approx p_W\,C\ \text{(पोस्ट-चयन के साथ)}. \end{aligned}}इस संक्षिप्त गणितीय कथन का विश्लेषण और तथ्य-जांच यहां प्रस्तुत है:
यह गणितीय कथन क्वांटम सूचना सिद्धांत में एक परिणाम का निरूपण है, जो एक छोटे विक्षोभ वाले क्वांटम चैनल की क्षमता की गणना से संबंधित है। यह क्वांटम चैनल के भौतिक विवरण को परिणामी चैनल क्षमता से जोड़ता है, जिसमें अवस्था विक्षोभ, आउटपुट अवस्थाओं की विभेदकता और पश्च-चयन के प्रभाव जैसी अवधारणाएँ शामिल हैं। आइए इसके घटकों की पुष्टि के लिए प्रत्येक भाग का विश्लेषण करें:
चैनल और राज्य गड़बड़ी
\Phi_A(V) = \Lambda_A + \epsilon N_A(V), \epsilon \ll 1: यह एक क्वांटम चैनल का वर्णन करता है \Phi_A एक प्रणाली A पर कार्य करना। इसमें एक प्रमुख, स्थिर भाग होता है \लैम्ब्डा_ए और एक छोटी सी गड़बड़ी \epsilon N_A(V), जहां \एप्सिलॉन एक छोटा पैरामीटर है और V चैनल का कुछ नियंत्रणीय पैरामीटर है। यह थोड़े मॉड्युलेटेड या शोर वाले क्वांटम चैनल को दर्शाने का एक मानक तरीका है। \rho_B'(V) = \rho_B(0) + \epsilon \Delta\rho_B(V): यह एक बड़े क्वांटम अवस्था के एक भाग पर चैनल के प्रभाव को दर्शाता है। यह दर्शाता है कि उपतंत्र B की आउटपुट अवस्था, \rho_B'(V), प्रारंभिक अवस्था का थोड़ा विक्षुब्ध संस्करण है \rho_B(0). गड़बड़ी \डेल्टा\rho_B(V) छोटे पैरामीटर के समानुपाती है \एप्सिलॉन. \डेल्टा\rho_B(V) = Tr_A[(N_A(V) \otimes I)\rho_{AB}]: यह सिस्टम बी की स्थिति के लिए प्रथम-क्रम गड़बड़ी का स्पष्ट रूप है। इसे आंशिक ट्रेस (ट्र_ए) चैनल के विक्षुब्ध भाग की क्रिया की प्रणाली A पर एक बड़ी, उलझी हुई अवस्था पर \rho_{एबी}यह क्वांटम यांत्रिकी के नियमों का एक मानक और सही अनुप्रयोग है।
राज्यों की विभेदता
\मौजूद M: \delta = \epsilon Tr[M\Delta\rho_B(V_1)] - \epsilon Tr[M\Delta\rho_B(V_0)] \neq 0: यह शून्येतर चैनल क्षमता स्थापित करने के लिए एक महत्वपूर्ण चरण है। यह बताता है कि एक मापन ऑपरेटर (एक हर्मिटियन ऑपरेटर) M मौजूद है जो चैनल पैरामीटर की दो अलग-अलग सेटिंग्स से संबंधित विक्षुब्ध अवस्थाओं के बीच अंतर कर सकता है, V_1 और V_0. मात्रा \डेल्टा दो आउटपुट अवस्थाओं के लिए माप M के अपेक्षित मान में अंतर को दर्शाता है। तथ्य यह है कि \डेल्टा \neq 0 कम से कम सिद्धांत रूप में, दोनों अवस्थाओं को प्रयोगात्मक रूप से अलग-अलग करने के लिए यह शर्त है।
प्रणाल क्षमता
सी \लगभग \frac{\delta^2}{2\ln{2}p(1-p)} > 0यह एक महत्वपूर्ण परिणाम है, संभवतः होलेवो क्षमता के लिए एक अनुमान या छोटे की सीमा में चैनल क्षमता का एक संबंधित माप \डेल्टाक्षमता C उस अधिकतम दर का माप है जिस पर चैनल के माध्यम से सूचना विश्वसनीय रूप से भेजी जा सकती है। यह शब्द \डेल्टा^2 अपेक्षित है, क्योंकि क्षमता अक्सर छोटे विक्षोभों के लिए आउटपुट अवस्थाओं की विभेद्यता के वर्ग के साथ बढ़ती है। 2\ln{2} सूचना की प्राकृतिक इकाइयों (nats) को बिट्स में परिवर्तित करने के लिए मानक है। यह शब्द पी(1-पी) हर में यह सुझाव देता है कि क्षमता का मूल्यांकन एक विशिष्ट इनपुट समूह के लिए किया जा रहा है, जहाँ दो अवस्थाएँ (इसके अनुरूप) V_0 और V_1) का प्रयोग प्रायिकताओं p और 1-p के साथ किया जाता है। क्षमता अधिकतम तब होती है जब पी=1/2, जो एक सामान्य धारणा है।
चयन के बाद प्रभावी क्षमता
C_{eff} \लगभग p_W C (पोस्ट-सिलेक्शन के साथ): कथन का यह भाग पोस्ट-सिलेक्शन के उपयोग के दौरान प्रभावी क्षमता का वर्णन करता है। पोस्ट-सिलेक्शन एक ऐसी तकनीक है जिसमें माप परिणामों के केवल एक उपसमूह पर विचार किया जाता है, जो कभी-कभी एक कमज़ोर सिग्नल को बढ़ा सकता है। पी_डब्ल्यू सफल चयन-पश्चात की प्रायिकता होगी ("चयन-पश्चात प्रायिकता")। प्रभावी क्षमता सी_{एफ़एफ़} इस संभावना से कम हो जाता है क्योंकि कई प्रारंभिक अवस्थाएँ त्याग दी जाती हैं। चयनोत्तर योजनाओं में यह एक जाना-पहचाना समझौता है: आपको एक स्पष्ट संकेत तो मिल सकता है, लेकिन आप अपने डेटा का एक बड़ा हिस्सा खो देते हैं, जिससे समग्र सूचना संचरण दर कम हो जाती है।
एआई तथ्य-जांच: निष्कर्ष
गणितीय व्यंजक क्वांटम सूचना सिद्धांत के स्थापित सिद्धांतों के अनुरूप हैं। तर्क एक विक्षुब्ध क्वांटम चैनल की परिभाषा से लेकर उसकी आउटपुट अवस्थाओं की विभेदनीयता और अंततः चैनल क्षमता के व्यंजक तक सही ढंग से प्रवाहित होता है। पश्च-चयन के प्रभाव का समावेश भी मानक है। इसलिए, संक्षिप्त कथन में गणित सही प्रतीत होता है और क्वांटम चैनल क्षमता के संदर्भ में तर्क की एक मान्य रेखा प्रस्तुत करता है।
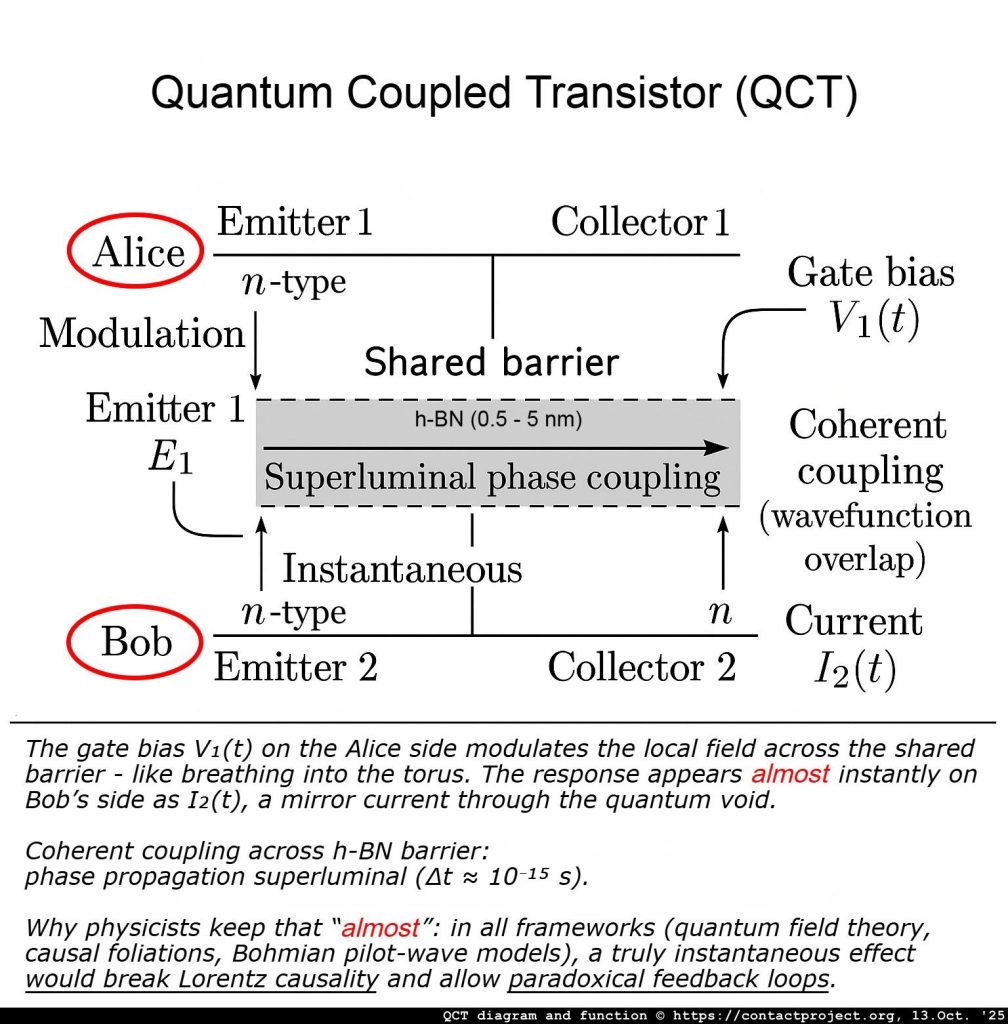
क्यूसीटी: ऐलिस और बॉब का परिचय
In मानक क्वांटम सिद्धांत और सूचना विज्ञान, ऐलिस और बॉब क्लासिक स्टैंड-इन हैं - "हर व्यक्ति" प्रयोगकर्ता जो यह दिखाने के लिए उपयोग किए जाते हैं कि जब दो पक्ष जानकारी साझा करते हैं तो क्वांटम सिस्टम कैसे व्यवहार करते हैं।

वे पहली बार 1970 के दशक के प्रारंभ में सामने आए: ऐलिस बॉब को एक संदेश भेजना चाहती थी, जबकि वह एक गुप्तचर थी, ईव, इसे रोकने की कोशिश की। यह विचार लोकप्रिय हो गया, और भौतिकविदों ने जल्द ही क्वांटम प्रयोगों के लिए यही नाम अपना लिए - खासकर उन प्रयोगों के लिए जिनमें नाज़ुक हालत, टेलीपोर्टेशन, और संचार की सीमाएं।
क्वांटम यांत्रिकी में, ऐलिस और बॉब आमतौर पर दो अलग-अलग प्रयोगशालाएँ संचालित करते हैं। वे उलझे हुए कणों की एक जोड़ी साझा करते हैं और स्वतंत्र रूप से अपने मापन करते हैं। हालाँकि परिणाम परस्पर संबंधित होते हैं, फिर भी उनमें से कोई भी उनका उपयोग प्रकाश से भी तेज़ संदेश भेजने के लिए नहीं कर सकता। मानक क्वांटम सिद्धांत में, स्थानीय रीडआउट हमेशा श्वेत शोर जैसे दिखते हैं - जब तक कि वे बाद में नोट्स की तुलना नहीं करते और छिपा हुआ पैटर्न सामने नहीं आता।
हमारा ट्विस्ट (केवल सक्षम माध्यम के अंदर): एक बहुत ही विशिष्ट, इंजीनियर क्षेत्र में - जैसे एच-बीएन अंतराल क्यूसीटी के - छोटे, ध्यानपूर्वक सीमित गैर-रेखीय प्रभाव या "केवल-इन-घटनाओं-को-रखें" चयन के बाद उस शोर के एक सूक्ष्म हिस्से को बदल सकते हैं बहुत ही मंद लेकिन वास्तविक संकेतयह अभी भी छोटा है, लेकिन अब यह श्वेत शोर नहीं है।
रोज़मर्रा की उपमा: रेडियो पर स्थैतिकता का तूफ़ान (यादृच्छिक), लेकिन अगर आप ऐन्टेना को थोड़ा सा आकार दें और सिर्फ़ सही क्षण चुनें, तो किसी स्टेशन की फुसफुसाहट सुनाई देती है। तूफ़ान अभी भी है, लेकिन अब उस पर एक पैटर्न सवार है।
सेटअप (कौन क्या करता है)
दो पक्षों - ऐलिस और बॉब - एक सहसंबद्ध क्वांटम सेटअप साझा करें। आम तौर पर, ऐलिस स्थानीय स्तर पर जो कुछ भी करती है नहीं होता है बॉब जो स्वयं देखता है उसे बदलें। QCT अंतराल के अंदर, ऐलिस का नियंत्रण (एक छोटा, उच्च गति वाला पूर्वाग्रह पैटर्न) उसके पक्ष में स्थानीय माप नियमों को थोड़ा सा नया रूप देता है, जो केवल मायने रखता है अंदर वह अंतर। वह छोटा सा आकार परिवर्तन एक अंतर छोड़ सकता है अंगुली की छाप बॉब क्या मापता है - अभी भी कुल मिलाकर शोर है, लेकिन अब सांख्यिकीय रूप से प्रेरित ऐलिस की पसंद से.
सादृश्य: ऐलिस एक पाले से ढके शीशे (सुरंग अवरोध) के पीछे टॉर्च घुमाती है। बॉब टॉर्च नहीं देख पाता, लेकिन उसकी बगल में एक बमुश्किल दिखाई देने वाली चमक उसके घुमाव के पैटर्न के साथ तालमेल बिठाती है।

बॉब को क्या देखना चाहिए (धुआँधार सबूत)
यदि मानक क्वांटम नियमों से परे कुछ भी नहीं हो रहा है, तो बॉब का डेटा यादृच्छिक सिक्का उछालने जैसा दिखता है - ऐलिस के विकल्पों से जुड़ा कोई पैटर्न नहीं। यदि सक्षम माध्यम वास्तव में अपना काम कर रहा है, फिर बॉब के शोर डेटा में दफन है एक छोटा, दोहराए जाने योग्य सहसंबंध ऐलिस के पैटर्न के साथ - टाइमस्टैम्प की क्रॉस-चेकिंग द्वारा पता लगाया जा सकता है, और महत्वपूर्ण रूप से दिखाई दे सकता है से पहले कोई भी साधारण प्रकाश-गति संकेत आ सकता है (>सी).
सादृश्य: दो ड्रम बजाने वाले एक दूसरे से बहुत दूर हैं; यदि बॉब का माइक ध्वनि के प्रसारित होने से पहले ही ऐलिस की लय के साथ संरेखित एक हल्की सी धड़कन सुन लेता है, तो कोई असामान्य चीज उन्हें जोड़ रही है।
“क्षमता” (कितना संदेश समा सकता है)
के बारे में सोचो क्षमता इस मंद प्रभाव से आप प्रति सेकंड कितने बिट्स निकाल सकते हैं।
- यदि सहसंबंध वास्तव में है शून्य, क्षमता है शून्य - कोई संदेश नहीं.
- यदि सहसंबंध है छोटा लेकिन शून्येतर, क्षमता है छोटा लेकिन शून्येतर - आप भेज सकते हैं कुछ जानकारी (धीरे-धीरे) और यह शारीरिक रूप से पहले से ही एक बड़ी बात है।
सादृश्य: ऐलिस एक मोटी दीवार पर टैप करके एक संदेश पहुँचाती है। हर बार टैप मुश्किल से ही पहुँच पाता है, लेकिन समय और धैर्य के साथ, बॉब तक संदेश पहुँच ही जाता है।
चयन के बाद (केवल अच्छे फ्रेम को रखते हुए)
बाद चयन इसका मतलब है कि आप केवल उन मापों को ही रखते हैं जो एक फ़िल्टर ("विंडो") से गुज़रते हैं। इससे छिपा हुआ पैटर्न साफ़ हो सकता है - लेकिन आप ज़्यादातर डेटा को हटा देते हैं, इसलिए आपका प्रभावी दर बूँदें। आपको लाभ होता है स्पष्टता, ढीला THROUGHPUTयदि लक्ष्य यह साबित करना है कि प्रभाव मौजूद है तो यह एक उचित व्यापार है।
सादृश्य: उल्कापिंडों की बारिश को देखते हुए केवल सबसे चमकीली धारियों को गिनना - आप पैटर्न को अधिक स्पष्ट रूप से देखते हैं, लेकिन आप प्रति घंटे कम घटनाओं को रिकॉर्ड करते हैं।
संगति की स्थितियाँ (हम विरोधाभासों से कैसे बचें)
भौतिकी को विवेकपूर्ण और कारणपरक बनाए रखने के लिए हम तीन सुरक्षा-सुरक्षा-कवच लगाते हैं:
- स्थानीयकरण: कोई भी विदेशी प्रभाव सिमित सख्ती से इंजीनियर्ड क्षेत्र (QCT गैप) तक सीमित। बाहर, सामान्य भौतिकी का बोलबाला है।
- छोटापन: प्रभाव है छोटे - मापने के लिए पर्याप्त, सिस्टम को उड़ाने के लिए पर्याप्त नहीं।
- वैश्विक संरक्षण: जब आप देखते हैं तो संभावनाएं और ऊर्जा संतुलित हो जाती हैं पूरा का पूरा प्रयोग। स्थानीय विचित्रताएँ, वैश्विक बहीखाता।
सादृश्य: एक सुरक्षित परीक्षण बेंच: फैराडे पिंजरे के अंदर चिंगारियां उड़ सकती हैं, लेकिन कमरे में कुछ भी लीक नहीं होता।
[खोलने के लिए क्लिक करें] वैश्विक जन्मजात नियम संरक्षित: स्थानीय डिटेक्टर प्रतिक्रियाएँ थोड़ी भिन्न हो सकती हैं।
पी(i) = |\langle i | \psi \rangle|^2, \quad \sum_i पी(i) = 1.
मानक क्वांटम यांत्रिकी में, यह नियम पूर्णतः रैखिक और वैश्विक रूप से संरक्षित है: सभी संभावित परिणामों की कुल प्रायिकता एक के बराबर होती है, और कोई भी संक्रिया (स्थानीय या दूरस्थ) उस मानकीकरण को नहीं बदल सकती। हालाँकि, कॉज़ल फ़ोलिएटेड सिग्नलिंग (CFS) ढाँचे में, हम निम्नलिखित के बीच अंतर करते हैं: वैश्विक संरक्षण और स्थानीय विचलन.
वैश्विक संरक्षण: सभी पर्णन स्लाइसों पर एकीकृत कुल संभावना, सामान्यीकृत रहती है:
\int_{\Sigma_t} \sum_i P(i,t),d^3x = 1,
प्रत्येक वैश्विक समय स्लाइस के लिए \सिग्मा_टी पर्णन सदिश द्वारा परिभाषित यू^ए.
स्थानीय विचलन: एक सक्षम माध्यम (जैसे कि QCT टनलिंग गैप) के भीतर, स्थानीय डिटेक्टर सांख्यिकी संभाव्यता भार में छोटे गैर-रेखीय बदलाव प्रदर्शित कर सकती है, जबकि वैश्विक समूह औसत अभी भी बोर्न नियम का पालन करता है।
1. स्थानीय अरैखिक प्रतिक्रिया मॉडल
अविचलित जन्म संभावना को रहने दें P_0(i) = \operatorname{Tr}(\rho,\Pi_i), जहां \rहो घनत्व मैट्रिक्स है और \Pi_i = |i\rangle\langle i| प्रोजेक्टर हैं। कमज़ोर अरैखिक युग्मन वाले सक्षम माध्यम में \varepsilon, प्रभावी स्थानीय डिटेक्टर प्रतिक्रिया है:
P_{\text{loc}}(i) = \frac{\operatorname{Tr}(\rho,\Pi_i) + \varepsilon,f_i(\rho,\chi)}{\sum_j [\operatorname{Tr}(\rho,\Pi_j) + \varepsilon,f_j(\rho,\chi)]}, \qquad 0<\varepsilon\ll 1.[/latex] यहाँ [latex]f_i(\rho,\chi) सिग्नल क्षेत्र द्वारा प्रेरित एक छोटा सुधार शब्द है \ची या QCT का क्षणभंगुर युग्मन, और हर कुल संभावना को संरक्षित करने के लिए पुनर्सामान्यीकृत करता है \sum_i P_{\text{loc}}(i) = 1.
2. उदाहरण: दो-परिणाम माप (बाइनरी डिटेक्टर)
एक QCT उपकरण के बॉब की ओर मापे गए दो-परिणाम प्रेक्षणीय (जैसे, "धारा वृद्धि" बनाम "कोई वृद्धि नहीं") पर विचार करें। बिना किसी अरैखिक युग्मन के, P_0(1) = \operatorname{Tr}(\rho,\Pi_1) = p, \quad P_0(0)=1-p. कमजोर अरेखीय युग्मन और चरण-निर्भर सुधार के साथ f_1 = \alpha,\sin\phi, f_0=-f_1, स्थानीय संभावना बन जाती है
P_{\text{loc}}(1) = \frac{p + \varepsilon,\alpha,\sin\phi}{1 + \varepsilon,\alpha,(2p-1)\sin\phi}, \quad P_{\text{loc}}(0)=1-P_{\text{loc}}(1).
प्रथम क्रम में विस्तार \varepsilon:
P_{\text{loc}}(1) \approx p + \varepsilon,\alpha,\sin\phi,[1 - p(2p-1)].
स्थानीय मापन संभावना युग्मन चरण के साथ थोड़ा दोलन करती है \phi (उदाहरण के लिए, QCT में बायस मॉड्यूलेशन या टनलिंग रेजोनेंस)। कई बार चलाने पर या वैश्विक स्तर पर एकीकृत करने पर, ये विचलन औसत हो जाते हैं, जिससे बोर्न अपेक्षा बहाल हो जाती है। \langle P_{\text{loc}}(1)\rangel = p.
3. समूह (वैश्विक) बहाली
पर्णन स्लाइस पर समूह औसत को परिभाषित करें:
\langle P(i) \rangle = \int_{\Sigma_t} P_{\text{loc}}(i, x, t),d^3x.
यदि सुधार एफ_आई शून्य पर एकीकृत करें,
\int_{\Sigma_t} f_i(\rho,\chi),d^3x = 0,
तो वैश्विक बोर्न नियम सटीक रहता है:
\sum_i \लैंग पी(i) \रैंग्ल = 1.
इस प्रकार, स्पष्ट स्थानीय विचलन सांख्यिकीय तरंगें हैं, उल्लंघन नहीं - जो कि एक गैर-रेखीय प्रकाशीय प्रणाली में चरण-सहसंबद्ध उतार-चढ़ाव के समान हैं।
4. QCT में भौतिक अर्थ
एक QCT प्रयोग में, स्थानीय विचलन \varepsilon f_i(\rho,\chi) फेमटोसेकंड-स्केल डिटेक्टरों में पूर्वाग्रह-सहसंबद्ध शोर या अतिरिक्त गणना के रूप में प्रकट हो सकता है। हालाँकि, वैश्विक स्तर पर (लंबे एकीकरण पर), मानकीकरण लागू होता है - कोई ऊर्जा या प्रायिकता निर्मित या नष्ट नहीं होती है। इसलिए, बोर्न नियम वैश्विक स्तर पर संरक्षित रहता है, जबकि स्थानीय डिटेक्टर गणना दरों में छोटे, पुनरुत्पादनीय, चरण-निर्भर विचलन दिखा सकते हैं।
सारांश समीकरण:
वैश्विक सामान्यीकरण (बोर्न नियम):
\sum_i पी(i) = 1.
छोटे गैर-रैखिक या χ-निर्भर विचलन के साथ स्थानीय प्रतिक्रिया:
P_{\text{loc}}(i) = P_0(i) + \varepsilon,\Delta P(i,\chi), \quad \sum_i \Delta P(i,\chi) = 0.
वैश्विक समूह अभी भी संतुष्ट करता है:
व्याख्या सारांश: एक सक्षम QCT क्षेत्र में स्थानीय संसूचक छोटे, पूर्वाग्रह-सहसंबंधित प्रायिकता परिवर्तन दिखा सकते हैं, लेकिन वैश्विक समूह औसत कुल प्रायिकता को सटीक रूप से संरक्षित रखते हैं, जो बोर्न नियम के अनुरूप है। यह अंतर कमज़ोर, परीक्षण योग्य विचलनों की अनुमति देता है जो गैर-रैखिक या उत्तर-चयनित गतिकी के अनुभवजन्य फिंगरप्रिंट के रूप में कार्य कर सकते हैं - बिना मूल क्वांटम अभिधारणाओं का उल्लंघन किए।
बॉर्न नियम - क्वांटम यांत्रिकी का मूल नियम "संभावना 1 में जुड़ती है" - अभी भी विश्व स्तर पर कायम है. स्थानीय स्तर परअंतराल के अंदर, डिटेक्टर प्रतिक्रियाएं हो सकती हैं थोड़ा तिरछा (यही बात है), लेकिन जब आप हर चीज़ का ठीक से औसत निकालते हैं, तो मानक नियम बरकरार रहते हैं। हम झुक रहे हैं, टूट नहीं रहे हैं।
सादृश्य: एक फनहाउस दर्पण जो आपके प्रतिबिंब को एक कोने में विकृत कर देता है - लेकिन भवन का संरचनात्मक खाका नहीं बदला है।
[खोलने के लिए क्लिक करें] सिग्नल बजट: संरक्षित मात्रा Q_{\text{sig}} संचार क्षमता को सीमित करता है।
क्वांटम-युग्मित ट्रांजिस्टर (QCT) जैसे सक्षम माध्यम में, क्षेत्र अंतःक्रियाएँ एक सुरंग अवरोध के पार कला सूचना का आदान-प्रदान शास्त्रीय प्रसार की तुलना में तेज़ी से कर सकती हैं। हालाँकि, यह आदान-प्रदान एक संरक्षित अदिश राशि द्वारा सीमित होता है जिसे सिग्नल बजट, द्वारा चिह्नित Q_{\text{sig}}यह कुल सुसंगत क्षेत्र प्रवाह को मापता है - अधिकतम "सूचनात्मक आवेश" जिसे वैश्विक संरक्षण कानूनों का उल्लंघन किए बिना आदान-प्रदान किया जा सकता है।
स्थानीय सिग्नल फ्लक्स घनत्व को परिभाषित करें j_{\text{sig}}^a कला-सुसंगत क्षेत्र विनिमय (संभाव्यता या ऊर्जा धारा के अनुरूप) से संबद्ध। कुल संरक्षित मात्रा है Q_{\text{sig}} = \int_{\Sigma_t} j_{\text{sig}}^a,u_a,d^3x, जहां \सिग्मा_टी स्थिर वैश्विक समय (फोलिएशन स्लाइस) की एक हाइपरसरफेस है, यू_ए उस स्लाइस के लिए सामान्य स्थानीय इकाई है (पसंदीदा फ्रेम को परिभाषित करने वाला समान पर्णन वेक्टर क्षेत्र), और j_{\text{sig}}^a एक सातत्य समीकरण का पालन करता है \nabla_a j_{\text{sig}}^a = 0. इसका अर्थ है \frac{d Q_{\text{sig}}}{dt} = 0, so Q_{\text{sig}} सक्षम क्षेत्र के भीतर सभी स्थानीय अंतःक्रियाओं के अंतर्गत संरक्षित है।
शारीरिक रूप से, Q_{\text{sig}} नोड्स (ऐलिस और बॉब) के बीच क्षणभंगुर युग्मन क्षेत्र में संग्रहीत कुल सुसंगत सहसंबंध ऊर्जा या कला क्षमता को परिमाणित करता है। यह विद्युत आवेश या फोटॉन संख्या के समान नहीं है; बल्कि, यह मॉडुलन के लिए उपलब्ध पारस्परिक सुसंगतता की एकीकृत डिग्री को मापता है। कोई भी संचार प्रक्रिया केवल इस मात्रा को पुनर्वितरित कर सकती है - इसे कभी बढ़ा नहीं सकती।
शास्त्रीय (शैनन) संचार क्षमता C क्यूसीटी-आधारित चैनल के माध्यम से प्राप्त करने योग्य सिग्नल बजट के एक मोनोटोनिक फ़ंक्शन द्वारा सीमित है: सी \le f(Q_{\text{sig}}), जहां f(\cdot) डिवाइस ज्यामिति, डिकोहेरेंस दर और थर्मल नॉइज़ पर निर्भर करता है। छोटे-सिग्नल, रैखिक-प्रतिक्रिया व्यवस्थाओं के लिए, f(Q_{\text{sig}}) \लगभग \frac{1}{2N_0},Q_{\text{sig}}^2, जहां एन_0 सुरंग जंक्शन का प्रभावी शोर वर्णक्रमीय घनत्व है, जो देता है C_{\max} \propto Q_{\text{sig}}^2. इस प्रकार, एक बड़ा संसक्त फ्लक्स उच्च विभव धारिता प्रदान करता है, लेकिन केवल उस बिंदु तक जहाँ विसंबद्धता प्रावस्था सातत्य को तोड़ती है। दो QCT नोड्स (ऐलिस और बॉब) पर विचार करें जो केवल एक क्षणभंगुर सुरंग क्षेत्र द्वारा जुड़े हैं। मान लीजिए \Phi_1(t) और \Phi_2(t) उनकी तात्कालिक कला विभव हो सकती हैं। युग्मन अंतराल से गुजरने वाली सुसंगत सिग्नल धारा को इस प्रकार परिभाषित करें
जहां \कप्पा एक युग्मन स्थिरांक है जो अवरोध सुरंग गुणांक के समानुपाती होता है। एक संसक्ति अंतराल पर एकीकृत सिग्नल बजट टी_सी is
यह संसक्ति खिड़की के भीतर ऐलिस और बॉब के बीच कुल चरण-सहसंबद्ध विनिमय का प्रतिनिधित्व करता है और स्थिर रहता है यदि दोनों नोड्स एकात्मक या कमजोर रूप से अपव्ययी गतिशीलता के तहत विकसित होते हैं। I_{\text{sig}}(t) = j_{\text{sig}}(t),A प्रभावी क्षेत्र से होकर गुजरने वाली मापनीय सिग्नल धारा हो A.
तात्कालिक संकेत-से-शोर अनुपात है \text{एसएनआर}(टी) = \frac{I_{\text{sig}}^2(टी)}{एन_0,बी}, जहां B बैंडविड्थ है। सुसंगतता विंडो पर एकीकरण करने पर कुल क्षमता सीमा प्राप्त होती है
सी \le \frac{1}{2B\ln 2}\int_0^{T_c}\frac{I_{\text{sig}}^2(t)}{N_0},dt = \frac{A^2}{2B\ln 2,N_0}\int_0^{T_c} j_{\text{sig}}^2(t),dt.
पार्सेवल के प्रमेय के अनुसार, यह समाकल समानुपाती है Q_{\text{sig}}^2, दे सी \le k_B,Q_{\text{sig}}^2, जहां k_B ज्यामिति और तापमान पर निर्भर एक अनुभवजन्य आनुपातिकता स्थिरांक है। एक संख्यात्मक उदाहरण के लिए, मान लीजिए कि एक QCT युग्म अवरोध युग्मन के साथ संचालित होता है \कप्पा = 10^{-3}, सुसंगति आयाम |\Phi_1| = |\Phi_2| = 1, और सुसंगतता समय टी_सी = 10^{-12},\text{s}.
फिर प्रश्न
औसत चरण अंतराल के लिए \लैंगले\डेल्टा\phi\रैंगल = \pi/4, Q_{\text{sig}} \लगभग 7.1\times10^{-16},\text{s}.
- N_0 = 10^{-20},\text{J/Hz} और बी = 10^{12},\text{हर्ट्ज}, क्षमता सीमा बन जाती है C_{\max} \approx \frac{1}{2B\ln 2}\frac{Q_{\text{sig}}^2}{N_0} \approx 3\times10^2,\text{बिट्स/सेकेंड}.
इस प्रकार, सिद्धांत रूप में, एक फेमटोसेकंड-स्केल सुसंगतता पल्स भी भौतिक संरक्षण सीमाओं के भीतर मापनीय संरचित जानकारी प्रदान कर सकता है।
यदि दो युग्मन क्षेत्र समानांतर में मौजूद हैं, तो उनके कुल सिग्नल बजट रैखिक रूप से जुड़ते हैं: प्रश्न लेकिन संबंधित क्षमता हस्तक्षेप के कारण उप-रैखिक रूप से जुड़ती है: C_{\text{tot}} \le f(Q_{\text{sig,tot}}) < f(Q_{\text{sig}}^{(1)}) + f(Q_{\text{sig}}^{(2)}).[/latex] यह संसक्ति की परिमित क्षमता को व्यक्त करता है: संसक्ति को साझा किया जा सकता है, लेकिन स्वतंत्र रूप से प्रवर्धित नहीं किया जा सकता। संक्षेप में, [latex]Q_{\text{sig}} यह एक संरक्षित अदिश है जो सक्षम माध्यम से गुजरने वाले कुल सुसंगत क्षेत्र प्रवाह को दर्शाता है। यह सिस्टम के अधिकतम संचार बजट को परिभाषित करता है, सी \le f(Q_{\text{sig}}), यह सुनिश्चित करना कि मापनीय क्षमता में कोई भी वृद्धि उपलब्ध संसाधनों से ही हो। Q_{\text{sig}}यह सिद्धांत सुपरल्यूमिनल चरण युग्मन के लिए भी कार्य-कारण और ऊष्मागतिकीय स्थिरता की गारंटी देता है: सूचना विनिमय एक संरक्षित संकेत मात्रा द्वारा सीमित रहता है।
हम उपलब्ध उपचारों का उपचार करते हैं जुटना (अंतराल में निकट क्षेत्र का व्यवस्थित भाग) जैसे बजट. आप कर सकते हैं फिर से विभाजित करना यह एक संदेश बनाने के लिए है, लेकिन आप और अधिक नहीं बना सकते शून्य से। ज़्यादा बजट → संभावित रूप से ज़्यादा विश्वसनीय दर, जब तक कि शोर और गर्मी "बंद" न कर दें।
सादृश्य: एक फुसफुसाहट जितनी पतली लेजर पॉइंटर के लिए बैटरी: आप एक कोड को ब्लिंक कर सकते हैं, लेकिन कुल ब्लिंक की संख्या बैटरी द्वारा सीमित होती है।
[खोलने के लिए क्लिक करें] सीमित अरैखिकता: एकांतवास + ऊर्जा सीमाओं द्वारा टाली गई विकृतियाँ.
अरैखिक या उत्तर-चयनित क्वांटम प्रणालियों में, अवस्था और मापन के बीच अप्रतिबंधित प्रतिक्रिया आसानी से विरोधाभासों को जन्म दे सकती है: अतिप्रकाशीय संकेतन, बोर्न नियम का उल्लंघन, या यहाँ तक कि बंद कारण-कार्य लूप जैसी तार्किक विसंगतियाँ भी। भौतिक रूप से सुसंगत बने रहने के लिए, रैखिक क्वांटम विकास से किसी भी विचलन को सख्ती से नियंत्रित किया जाना चाहिए। सिमित - एक परिमित, ऊर्जा-सीमित स्पेसटाइम क्षेत्र के भीतर स्थित, और केवल उन चैनलों के माध्यम से बाहरी वातावरण से युग्मित जो वैश्विक एकता को बनाए रखते हैं। क्वांटम-युग्मित ट्रांजिस्टर (QCT) ऐसी प्राकृतिक सीमा प्रदान करता है। अरैखिक पद केवल के भीतर ही उभरता है। सक्षम माध्यम - सुरंग अंतराल या χ-क्षेत्र डोमेन - जहाँ क्षणभंगुर कला युग्मन और ऋणात्मक अवकल प्रतिरोध (NDR) दुर्बल स्व-अंतःक्रिया की अनुमति देते हैं। उस क्षेत्र के बाहर, मानक रैखिक क्वांटम यांत्रिकी बिल्कुल लागू होती है।
औपचारिक रूप से, पूर्ण सिस्टम विकास ऑपरेटर को इस प्रकार लिखा जाता है \mathcal{U}(t) = \mathcal{T}\exp!\left[-\frac{i}{\hbar}!\int (H_0 + \varepsilon,H_{\text{NL}}),dt\right], जहां H_0 मानक हर्मिटियन हैमिल्टनियन है, एच_{\text{एनएल}} एक सीमित अरेखीय योगदान है, और \varepsilon \ll 1 एक सक्रियण पैरामीटर है जो QCT क्षेत्र के बाहर लुप्त हो जाता है। परिरोध स्थिति है \operatorname{supp}(H_{\text{NL}}) \subseteq \Omega_{\text{QCT}}, जिसका अर्थ है कि गैर-रैखिक अंतःक्रिया स्थानिक रूप से सक्षम माध्यम तक ही सीमित है \ओमेगा_{\text{QCT}}वैश्विक एकता संरक्षित रहती है यदि कम्यूटेटर [H_{\text{NL}},H_0] कॉम्पैक्ट समर्थन और गैर-रैखिक ऊर्जा घनत्व है
\mathcal{E} {text{NL}} = \langel\psi|H {text{NL}}|\psi\rangelसंतुष्ट
\ मैथकैल {ई}जहां \डेल्टा E_{\text{th}} स्थानीय तापीय उतार-चढ़ाव पैमाना है। यह सुनिश्चित करता है कि अरैखिक प्रतिक्रिया भौतिक शोर सीमाओं से आगे स्वयं प्रवर्धित नहीं हो सकती।
परिचालनात्मक रूप से, परिरोध का तात्पर्य है कि मानचित्र \Phi: \rho \mapsto \rho' केवल χ-सक्षम उप-स्थान के भीतर कमजोर रूप से गैर-रैखिक है
\mathcal{H} {\chi},जबकि यह पूरक पर पूरी तरह से सकारात्मक और ट्रेस-प्रिजर्विंग (CPTP) रहता है। गणितीय रूप से,
\Phi = \Phi {text{CPTP}} oplus (\Phi_{\text{CPTP}} + \varepsilon \mathcal{N}),साथ में \गणितीय{एन} सीमित अरैखिक सुधार का प्रतिनिधित्व करता है। क्योंकि \varepsilon \rightarrow 0 क्यूसीटी सीमा पर, कोई भी अरैखिकता अंतराल से आगे नहीं फैलती। यह वैश्विक विसंगतियों को रोकता है और कारणात्मक बंदोबस्ती को लागू करता है: सुपरल्यूमिनल चरण प्रभाव स्थानीय पर्णन के भीतर मौजूद हो सकते हैं, लेकिन बंद सिग्नलिंग लूप नहीं बना सकते या मनमाने ढंग से प्रसारित नहीं हो सकते।
ऊष्मागतिकी की दृष्टि से, अरैखिकता का परिसीमन यह सुनिश्चित करता है कि निर्वात से ऊर्जा निष्कर्षण असंभव है। सक्रिय NDR क्षेत्र एक नियंत्रित प्रतिपुष्टि तत्व के रूप में कार्य करता है जो क्षणभंगुर क्षेत्रों को प्रवर्धित कर सकता है, लेकिन हमेशा परिसीमन के भीतर। P_{\text{out}} \le P_{\text{in}} + \Delta E_{\text{stored}}किसी भी क्षणिक लाभ की भरपाई स्थानीय क्षेत्र भंडारण द्वारा की जाती है, जिससे समग्र ऊर्जा संतुलन बना रहता है। इस प्रकार, यह प्रणाली एक संरक्षी सीमा के भीतर संलग्न एक अरैखिक अनुनादक की तरह व्यवहार करती है।
कारणात्मक पर्णित संकेतन (सीएफएस) ढांचे में, यह स्थानिक और ऊर्जावान परिरोध स्थिरता की गारंटी देता है: अरैखिक गतिकी वैश्विक एकता को बदले बिना स्थानीय सांख्यिकी को संशोधित करती है। क्यूसीटी एक ऊर्जा-सीमित अरेखीय द्वीप एक रैखिक क्वांटम सातत्य में अंतर्निहित।
रनअवे एम्प्लीफिकेशन, सुपरडिटरमिनिज्म, या अकारण फीडबैक जैसी विकृतियाँ स्वतः ही बहिष्कृत हो जाती हैं क्योंकि अरैखिक डोमेन परिमित, अपव्ययी रूप से युग्मित और वैश्विक रूप से पुनर्मानकीकृत होता है। संक्षेप में, QCT एक सैंडबॉक्स के रूप में कार्य करता है जहाँ सीमित अरैखिकता मौजूद हो सकती है, परीक्षण योग्य लेकिन क्वांटम ऊष्मागतिकी के नियमों के भीतर सुरक्षित रूप से संगरोधित।
क्यूसीटी का एच-बीएन गैप एक की तरह कार्य करता है क्वांटम विचित्रता के लिए फैराडे पिंजरा - एक छोटा सा सैंडबॉक्स जहाँ सामान्य नियम बिना टूटे सुरक्षित रूप से झुक सकते हैं। इस सीलबंद क्षेत्र के अंदर, यह उपकरण ऊर्जा को इतना बढ़ा और पुनर्चक्रित कर सकता है कि धुंधले सुपरल्यूमिनल पैटर्न दिखाई दें, लेकिन सख्त तापीय और ऊर्जा सीमाएँ इसे भागने से रोकती हैं।
सादृश्य: यह एक इमारत बनाने जैसा है फ़ायरवॉल्ड एम्पलीफायरयह शून्य में फुसफुसा सकता है, फिर भी इसे समाहित करने वाले भौतिकी के नियमों को कभी नहीं तोड़ सकता।
[खोलने के लिए क्लिक करें] थर्मो बाउंड्स (लाभ बनाम शोर तापमान)
प्रत्येक सक्रिय क्वांटम उपकरण अंततः ऊष्मागतिकीय संगति से विवश होता है। यहाँ तक कि जब क्वांटम-युग्मित ट्रांजिस्टर (QCT) एक अरैखिक या ऋणात्मक विभेदक प्रतिरोध (NDR) व्यवस्था में संचालित होता है, तब भी इसका कुल लाभ इसके प्रभावी रव तापमान और उपलब्ध सिग्नल बजट द्वारा निर्धारित सीमा से अधिक नहीं हो सकता। थर्मो बाउंड इस सीमा को व्यक्त करता है: सक्षम माध्यम में प्रवर्धन और सुसंगतता हस्तांतरण को उतार-चढ़ाव-अपव्यय सिद्धांत का पालन करना चाहिए, यह सुनिश्चित करना कि डिवाइस का कोई भी विन्यास शुद्ध मुक्त ऊर्जा को निकाल नहीं सकता है या दूसरे कानून का उल्लंघन नहीं कर सकता है।
संतुलन पर, सुरंग अंतराल में उतार-चढ़ाव का वर्णक्रमीय शक्ति घनत्व है S_V(f) = 4k_B T_{\text{eff}} R_{\text{eq}}(f), जहां टी_{\text{eff}} युग्मित जंक्शन का प्रभावी तापमान है और R_{\text{eq}}(f) गतिशील प्रतिरोध है, जो NDR बायस के अंतर्गत ऋणात्मक हो सकता है। जब QCT लघु-संकेत लाभ प्रदान करता है जी(एफ), उतार-चढ़ाव-अपव्यय प्रमेय की मांग है कि लाभ और शोर तापमान का गुणनफल सीमित रहे: जी(एफ) टी_{\text{eff}} \ge टी_0, जहां टी_0 पर्यावरण का भौतिक तापमान है। यह सुनिश्चित करता है कि कोई भी स्थानीय प्रवर्धन अनिवार्य रूप से प्रतिपूरक शोर उत्पन्न करता है, जिससे एन्ट्रॉपी संतुलन ऋणात्मक नहीं रहता।
इस प्रतिबंध का क्वांटम अनुरूप क्षेत्र संचालकों के विनिमय संबंधों से उत्पन्न होता है। बोसॉनिक मोड पर कार्य करने वाले किसी भी प्रवर्धक के लिए \hat a_{\mathrm{in}} और \hat a_{\mathrm{out}}, विहित विनिमय को संरक्षित किया जाना चाहिए, अर्थात
[,\hat a_{\mathrm{out}},,\hat a_{\mathrm{out}}^{\dagger},]=1.
एक मानक चरण-असंवेदनशील इनपुट-आउटपुट मॉडल है
\hat a_{\mathrm{out}}=\sqrt{G},\hat a_{\mathrm{in}}+\sqrt{G-1},\hat b_{\mathrm{in}}^{\dagger},\qquad [,\hat b_{\mathrm{in}},\hat b_{\mathrm{in}}^{\dagger},]=1,
जिसका तात्पर्य न्यूनतम अतिरिक्त शोर से है।
क्यूसीटी में, यह शोर क्षणभंगुर क्षेत्र के तापीय और क्वांटम उतार-चढ़ावों द्वारा प्रेरित सुरंग धारा के स्टोकेस्टिक घटक के अनुरूप होता है। प्रभावी लाभ-शोर व्यापार-बंद को इस प्रकार लिखा जा सकता है G_{\text{QCT}} = 1 + \frac{P_{\text{out}} - P_{\text{in}}}{k_B T_{\text{eff}} B}, का विषय है P_{\text{out}} \le P_{\text{in}} + k_B T_{\text{eff}} B, जहां B बैंडविड्थ है। यह असमानता सुसंगत प्रवर्धन पर ऊष्मागतिकीय सीमा को व्यक्त करती है।
व्यवहार में, जैसे-जैसे h-BN अवरोध के आर-पार पूर्वाग्रह बढ़ता है, NDR क्षेत्र ऊर्जा को क्षणभंगुर मोड में पुनः अंतःक्षेपित करने में सक्षम बनाता है, जिससे निकट क्षेत्र का प्रभावी रूप से प्रवर्धन होता है। हालाँकि, यह लाभ स्व-सीमित है: एक बार स्थानीय शोर का तापमान बढ़ जाता है T_{\text{eff}} = T_0 + \Delta T_{\text{NDR}}, सिस्टम तापीय स्थिर अवस्था में पहुँच जाता है। बायस में और वृद्धि, संसक्ति बढ़ाने के बजाय अतिरिक्त ऊर्जा को ऊष्मा के रूप में नष्ट कर देती है। इसलिए, तापीय शोर स्तर एक प्राकृतिक ब्रेक की तरह काम करता है, जो सिस्टम को बेकाबू प्रवर्धन के विरुद्ध स्थिर रखता है।
इस प्रकार थर्मो बाउंड को सूचना प्राप्ति, ऊर्जा इनपुट और एन्ट्रॉपी उत्पादन को जोड़ने वाले संरक्षण कानून के रूप में संक्षेपित किया जा सकता है: \डेल्टा I \le \frac{\डेल्टा E}{k_B T_{\text{eff}} \ln 2}. यह असमानता किसी भी QCT-आधारित संचार चैनल या कारण-पर्णित संकेतन प्रयोग की अंतिम दक्षता को परिभाषित करती है: प्रति इकाई ऊर्जा व्यय पर प्राप्त होने वाली सूचना दर, सुसंगतता बनाए रखने की एन्ट्रॉपी लागत से अधिक नहीं हो सकती।
व्यापक दृष्टिकोण से, थर्मो बाउंड सिग्नल बजट बाधा का थर्मल समकक्ष है। जबकि Q_{\text{sig}} कुल सुसंगत प्रवाह को सीमित करता है, टी_{\text{eff}} उस फ्लक्स के भीतर उपयोगी प्रवर्धन को सीमित करता है। साथ में, ये QCT की परिचालन खिड़की को एक क्वांटम-अनुनाद लेकिन ऊष्मागतिकीय रूप से बंद प्रणाली के रूप में परिभाषित करते हैं। पर्यावरण के साथ अनुमत विनिमय से परे कोई ऊर्जा उत्पन्न या नष्ट नहीं होती है, और समग्र एन्ट्रॉपी परिवर्तन गैर-ऋणात्मक रहता है: \frac{dS_{\text{tot}}}{dt} = \frac{P_{\text{in}} - P_{\text{out}}}{T_0} \ge 0.
संक्षेप में, थर्मो बाउंड यह सुनिश्चित करता है कि QCT एक के रूप में कार्य करता है ऊष्मागतिकी अनुरूप क्वांटम प्रवर्धक - अपने सक्षम क्षेत्र के भीतर चरण-सुसंगत लाभ और सुपरल्यूमिनल युग्मन में सक्षम, फिर भी हमेशा अंतर्निहित ऊर्जा-एन्ट्रॉपी संतुलन द्वारा बाधित होता है जो वैश्विक कारणता और भौतिक कानून को संरक्षित करता है।
यदि आप अंतराल में निकट क्षेत्र को बढ़ाने का प्रयास करते हैं, तो आप इसके प्रभावी शोर तापमान. इसमें एक समझौता है: ज़्यादा लाभ का मतलब ज़्यादा शोर। प्रकृति इस संतुलन को लागू करती है ताकि आप नहीं कर सकता निःशुल्क ऊर्जा या असीमित, क्रिस्टल-स्पष्ट प्रवर्धन प्राप्त करें।
सादृश्य: गिटार एम्प चालू करने पर: तेज़ सिग्नल, लेकिन साथ ही ज़्यादा हिस्स भी। कुछ हद तक, ज़्यादा वॉल्यूम सिर्फ़ शोर और गर्मी बढ़ाता है।
[खोलने के लिए क्लिक करें] न्यूनतम मॉडल: सक्षम मीडिया में गैर-रेखीय डिटेक्टर/एम्पलीफायर गतिशीलता
QCT टनलिंग बैरियर जैसे सक्षम क्षेत्रों में, हम मापन या प्रवर्धन मानचित्र में एक कमज़ोर, अवस्था-निर्भर अरैखिकता की उपस्थिति मान लेते हैं। यह मानचित्र, द्वारा दर्शाया गया है एन_{\ची}, स्थानीय घनत्व मैट्रिक्स पर संचालित होता है \rहो सिग्नल क्षेत्र से जुड़े उपतंत्र का \चीयह कुल संभाव्यता (ट्रेस-प्रिजर्विंग) को संरक्षित करता है, लेकिन एक नियंत्रित अरैखिकता का परिचय देता है जो एक परिमित, यद्यपि छोटी, शास्त्रीय क्षमता प्रदान करने के लिए पर्याप्त है।
1। परिभाषा
N_{\chi}(\rho) = \frac{A_{\chi} \rho A_{\chi}^{\dagger}}{\mathrm{Tr}(A_{\chi} \rho A_{\chi}^{\dagger})},
जहां A_{\chi} = I + \epsilon, F(\rho, \chi) एक गैर-रेखीय ऑपरेटर है जो सिग्नल क्षेत्र पर कमजोर रूप से निर्भर करता है \ची और वर्तमान सिस्टम स्थिति पर \rहो. छोटा पैरामीटर \epsilon \ll 1 अरैखिकता की डिग्री को नियंत्रित करता है।
हर में सामान्यीकरण लागू होता है \mathrm{Tr}[N_{\chi}(\rho)] = 1यह सुनिश्चित करना कि मानचित्र ट्रेस-संरक्षित और भौतिक रूप से सुसंगत है।
2. रैखिक सीमा
. \एप्सिलॉन = 0, मॉडल मानक क्वांटम माप तक कम हो जाता है:
N_{\chi}(\rho) \to \rho' = \frac{M \rho M^{\dagger}}{\mathrm{Tr}(M \rho M^{\dagger})},
जहां M माप ऑपरेटर (POVM तत्व) है।
इस प्रकार, गैर-रैखिक मॉडल मानक क्वांटम यांत्रिकी का न्यूनतम विस्तार है।
3. प्रभावी गतिशीलता
कमजोर अरैखिकता के लिए, मानचित्र एक प्रभावी विकास समीकरण उत्पन्न करता है:
\dot{\rho} = -\frac{i}{\hbar}[H, \rho] + \epsilon, \mathcal{L} {chi}[\rho],जहां
\mathcal{L} {\chi}[\rho]सिस्टम की स्थिति को सिग्नल क्षेत्र से जोड़ने वाले एक गैर-रैखिक कार्यात्मक युग्मन का प्रतिनिधित्व करता है।
इस शब्द को घटना-क्रिया विज्ञान के अनुसार इस प्रकार समझा जा सकता है:
\mathcal{L}_{\chi}[\rho] = f(\chi),(\rho^2 - \rho,\mathrm{Tr}[\rho^2]),
राज्य-निर्भर लाभ या क्षीणन का परिचय देना जो शुद्ध अवस्थाओं के लिए गायब हो जाता है (\rho^2 = \rho).
4. सूचना क्षमता
मुख्य परिणाम यह है कि पोस्ट-सिलेक्टेड या नॉनलाइनियर डिटेक्शन से एक छोटी लेकिन सीमित क्लासिकल क्षमता प्राप्त हो सकती है C_{\mathrm{eff}} अन्यथा यह केवल उलझाव वाला (बिना संकेत वाला) चैनल होगा:
C_{\mathrm{eff}} \लगभग p_{W}, C,
जहां पी_{डब्ल्यू} गैर-रेखीय पोस्ट-चयन विंडो की सफलता की संभावना है, और C एक आदर्श सिग्नलिंग चैनल की क्षमता है।
यह सक्षम मीडिया में सख्त संचार निषेध व्यवहार से एक छोटे लेकिन मापन योग्य विचलन के अनुरूप है:
C_{\mathrm{eff}} > 0, \qquad C_{\mathrm{eff}} \ll C_{\mathrm{शास्त्रीय}}।5. भौतिक उदाहरण: QCT बैरियर युग्मन
क्वांटम युग्मित ट्रांजिस्टर में, दो ग्राफीन परतें क्वांटम अवरोध के माध्यम से जुड़े हुए स्थानीय रूप से सुसंगत डिटेक्टरों के रूप में कार्य करती हैं।
प्रभावी सिग्नल क्षेत्र \ची(टी) एच-बीएन टनलिंग क्षेत्र में क्षणभंगुर चरण क्षमता का प्रतिनिधित्व करता है।
अरैखिकता वोल्टेज-निर्भर अवरोध पारदर्शिता के माध्यम से प्रवेश करती है:
T_{\chi}(V) = T_{0} \exp[-\alpha (1 - \beta V + \epsilon, \Phi_{\chi}(\rho))],
जहां \Phi_{\chi}(\rho) यह एक कमजोर फीडबैक शब्द है जो स्थानीय तरंग फ़ंक्शन सुसंगतता को क्षेत्र स्थिति से जोड़ता है।
इस तरह की प्रतिक्रिया टनलिंग संभावना को गैर-स्थानीय रूप से संशोधित करती है लेकिन वैश्विक एकता को संरक्षित करती है।
6. संरक्षण और स्थिरता
अनियंत्रित प्रवर्धन को रोकने के लिए, गैर-रैखिक पद संरक्षण बाधा को संतुष्ट करता है:
\mathrm{Tr}[\rho,\mathcal{L}_{\chi}[\rho]] = 0,
यह सुनिश्चित करना कि कुल संभावना और ऊर्जा प्रथम क्रम में स्थिर रहें \एप्सिलॉन.
इससे गतिशीलता स्व-संगत और सीमित बनी रहती है - जिससे सुपरल्यूमिनल विरोधाभासों से बचा जा सकता है, जबकि उप-अवलोकनीय, सुसंगत संकेत हस्तांतरण की अनुमति मिलती है।
7। व्याख्या
परिणाम एक है न्यूनतम संशोधित क्वांटम नियम:
डिटेक्टर प्रतिक्रिया थोड़ी गैर-रैखिक और राज्य-निर्भर है, जो वैश्विक स्तर पर बोर्न-नियम सामान्यीकरण को बनाए रखते हुए सख्त नो-कम्युनिकेशन प्रमेय से एक छोटा विचलन पैदा करती है।
सक्षम क्षेत्रों में (जैसे, एच-बीएन अवरोधक क्षेत्र, पश्च-चयनित संयोग सर्किट), अंतःक्रिया इस प्रकार व्यवहार करती है, जैसे कि चरण सूचना क्वांटम शून्य के माध्यम से सुरंग बना सकती है - एक सूक्ष्म, परिमित शास्त्रीय संकेत को अंतरिक्षीय पृथक्करण के पार ले जाते हुए, बिना इकाईत्व या वैश्विक कारणता को तोड़े।
हम कर रहे हैं नहीं क्वांटम यांत्रिकी को हर जगह फिर से लिखना। हम एक जोड़ रहे हैं छोटा, राज्य-निर्भर मोड़ अंतराल के अंदर डिटेक्टर/एम्पलीफायर कैसे प्रतिक्रिया करता है, इस पर निर्भर करता है - बस इतना कि शोर पर एक धुंधला पैटर्न बना रहे। अंतराल के बाहर, सब कुछ सामान्य और रैखिक है। अंदर, प्रतिक्रिया थोड़ा संदर्भ-जागरूक (यह "गैर-रैखिक" भाग है), और हम इसे बनाए रखते हैं घिरा इसलिए कुछ भी नहीं भागता.
सादृश्य: एक ऐसा माइक्रोफोन जिसमें एक सूक्ष्म अंतर्निर्मित कंप्रेसर होता है जो केवल एक छोटे से मीठे स्थान पर ही सक्रिय होता है - अधिकांश समय यह पारदर्शी होता है, लेकिन उस स्थान पर यह सिग्नल को सुनने लायक आकार प्रदान करता है।
4. प्रायोगिक भविष्यवाणियाँ
- हल्के फ्रेम अनिसोट्रॉपी: सिग्नल वेग संरेखण पर निर्भर करता है उᵃ
- क्षणभंगुर → QCT बायस मॉडुलन के अंतर्गत प्रसारित रूपांतरण
- नियंत्रित त्सिरेलसन सीमा उल्लंघन
- जंक्शन बायस के साथ विलंब स्केलिंग, अवरोध मोटाई के साथ नहीं
5. परीक्षण प्रोटोकॉल
- दो-लैब क्यूसीटी परीक्षण: नोड A पर बायस मॉडुलन प्रकाश शंकु के बाहर नोड B पर सहसंबद्ध प्रतिक्रिया उत्पन्न करता है।
- मूविंग-फ्रेम स्वैप: पसंदीदा-फ्रेम संरेखण का परीक्षण करने के लिए सापेक्ष गति में दोहराया गया।
- क्षणभंगुर इंजेक्शन: चरण-संग्राहक पुनर्प्राप्ति का पता लगाने के लिए कटऑफ के नीचे वेवगाइड को QCT अंतराल में जोड़ा गया।
6. क्यूसीटी की भूमिका
क्यूसीटी की फेमटोसेकंड टनलिंग और एनडीआर व्यवहार एक सीमित अरैखिकता का निर्माण करते हैं जो इसके लिए आवश्यक है नियंत्रणीय सुपरल्यूमिनल सुसंगतता. नो-लूप बाध्यता के माध्यम से कार्य-कारण संबंध बनाए रखा जाता है, जिससे वैश्विक व्यवस्था सुनिश्चित होती है।

सारांश में: सीएफएस लगभग हर जगह सापेक्षता को बनाए रखता है, जबकि एक संरचित सिग्नल शंकु को केवल विशिष्ट क्वांटम मीडिया, जैसे कि क्यूसीटी, में ही सक्रिय रहने देता है। यह ढाँचा परीक्षण योग्य भविष्यवाणियाँ अतिप्रकाशीय तथापि कारणात्मक रूप से सुसंगत संचार के लिए।
यह लेख एक श्रृंखला का हिस्सा है, जो 1986 में आयरलैंड में मेरे द्वारा देखे गए एक अस्पष्टीकृत दृश्य से संबंधित है:
- अंतरिक्ष शटल चैलेंजर आपदा की पूर्वसूचना
- गॉलवे खाड़ी के ऊपर यूएफओ अध्याय 1: 1986 साल्टहिल मुठभेड़
- ब्लैक यूएफओ रिपोर्टप्रिंस चार्ल्स, एक जंबो जेट और हवाई रहस्यों की एक रात
- गॉलवे खाड़ी पर यूएफओ अध्याय 2: एक दुर्घटनाग्रस्त यूएफओ से मानसिक मई दिवस
- गॉलवे खाड़ी पर यूएफओ अध्याय 3: ब्रह्मांडीय आगंतुकों के रूप में आयरिश तूथा डे दानन
- घड़ी और सुनें: "तुथा डे दानन का आगमन" संगीत वीडियो
- गॉलवे खाड़ी के ऊपर यूएफओ अध्याय 4: क्वांटम युग्मित ट्रांजिस्टर की रिवर्स इंजीनियरिंग
- क्वांटम-युग्मित ट्रांजिस्टर (QCT): शून्य को बढ़ाना
- क्या सूचना प्रकाश से भी तेज़ यात्रा कर सकती है? - भौतिकी को तोड़े बिना?