🕔 Geschätzte Lesezeit: 32 Minuten
Die Logik der kausal-folierten Signalgebung
Die Theorie von Kausal-Foliated Signaling (CFS) schlägt vor, dass die Zeit verborgene Schichten enthält, die eine begrenzte Kohärenz zwischen Quantensystemen ermöglichen, die schneller als Licht ist. Forscher könnten bald die Quantengekoppelter Transistor (QCT) – ein Nanogerät mit zwei Graphenen – um diese Effekte direkt zu testen und festzustellen, ob sie auftreten können, ohne die bekannten Gesetze der Physik zu verletzen.
Im Kern stellt CFS eine provokante Frage: Was wäre, wenn bestimmte Arten von Wellen, wie etwa evaneszente oder Nahfeldwellen, Phaseninformationen schneller als Licht austauschen und dennoch die Kausalität bewahren könnten?
Wenn das zutrifft, ist die Raumzeit möglicherweise nicht vollkommen einheitlich. Sie könnte eine subtile innere Struktur aufweisen – eine „Schichtung“ der Zeit, bei der die Informationen innerhalb jeder Schicht leicht vorrücken, im Großen und Ganzen aber konsistent bleiben.

In dieser Sichtweise entfaltet sich das Universum wie die Seiten eines riesigen kosmischen Buches: Jede Seite wird in perfekter Reihenfolge umgeblättert, auch wenn manche Seiten etwas schneller umblättern als andere. CFS bietet eine verfeinerte Vision der Relativitätstheorie – eine, die strukturierte überlichtschnelle Kohärenz ermöglicht und gleichzeitig die Geschichte von Ursache und Wirkung intakt hält.
Teil II. Kausal-Foliated Signaling (CFS)
- Kernaxiome
- Kinematik und Dynamik
- Quantenregeln und Erhaltung
- Experimentelle Vorhersagen
- Testprotokolle
- Rolle des QCT
1. Kernaxiome
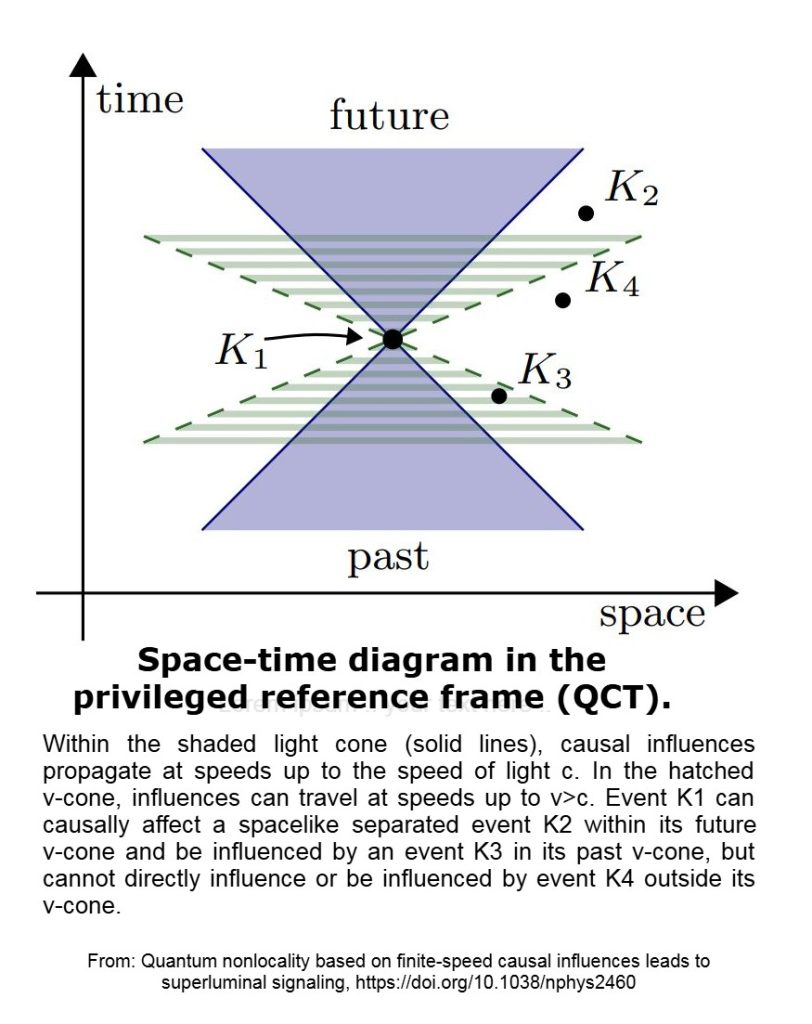
- Globale Zeitblätterung: Die Raumzeit besitzt eine bevorzugte globale Aufteilung (kosmische Zeit, definiert durch zeitartige Vektoren uᵃ). Alle Signale – luminale und superluminale – werden durch diese Blätterung geordnet.
- Vergrößerter Signalkegel: Über den Lichtkegel hinaus existiert für bestimmte Medien oder Felder ein breiterer „Signalkegel“ (χ).
- Chronologieschutz: Geschlossene Signalschleifen sind aufgrund von Lösbarkeitsbeschränkungen dynamisch verboten.
- Einsatzort: Standardexperimente bleiben Lorentz-invariant; Abweichungen treten nur innerhalb aktivierter Medien auf.
2. Kinematik und Dynamik
- Bevorzugter Rahmen: Ungefähr auf das CMB-Ruhesystem ausgerichtet.
- Signalfeld (χ): Koppelt schwach an EM-Träger und erweitert den Kausalkegel.
- Überlichtschnelle Eigenschaften: PDE in aktivierten Medien zeigen Ausbreitung außerhalb des g-Lichtkegels.
- Keine Schleifenbeschränkung: Integrale Bedingungen verhindern zeitverkürzende Kausalschleifen.
3. Quantenregeln und Erhaltung
Wir haben einen winzigen Bereich (die QCT-Lücke) geschaffen, in dem Quantennahfelder sanft geformt werden können, so dass ein kaum wahrnehmbares, schnelleres als Licht Anleitungen taucht in ansonsten zufälligen Daten auf – klein genug, um die Physik sicher zu halten, klar genug, um im Labor getestet zu werden.

Wenn die kompakte Aussage oben für Sie Sinn macht, können Sie die redlined Quantenregeln Klicken Sie unten auf die schwarzen ▶ Dreiecke, um eine ausführlichere Diskussion zu erhalten.
Für allgemeine Leser enthält jeder Abschnitt eine kurze Erklärung (ohne Mathematik), gefolgt von einer Analogie. Obwohl die meisten Menschen noch nie von der Nicht-Kommunikationstheorem (Verhindert die Kommunikation mit Überlichtgeschwindigkeit … durch Verschränkung), wird es hier aufgrund seiner grundlegenden Bedeutung hervorgehoben, und weil ein gesteuert Entspannung dieser Regel wird hier untersucht.
[zum Öffnen klicken] Entspannter Nicht-Kommunikationssatz: In aktivierten Medien ermöglichen nichtlineare/nachselektierte Dynamiken eine winzige klassische Kapazität > 0.
Anspruch (operativ):
In einem aktiviertes Medium (z. B. eine QCT-Lücke, die als χ-fähiges Nahfeld fungiert), ein schwache, lokalisierte Nichtlinearität or explizite Nachauswahl kann produzieren kleine, aber endliche klassische Kapazität C>0 zwischen raumartig getrennten Parteien, ohne die globale Unitarität oder die Born-Regel zu verletzen.
Einrichtung
Lassen ρAB ein bipartiter Zustand sein, der von Alice und Bob geteilt wird. In der Standard-QM mit lokalem CPTP-Karten und nicht Nach der Auswahl ist Bobs reduzierter Zustand unabhängig von Alices Wahl:
ρB′=TrA[(ΦA⊗IB)(ρAB)]=ρB, (keine Signalisierung)
In einem freigegeben QCT-Region, Modell Alices kontrollierter Betrieb als schwach nichtlinear Störung einer CPTP-Karte:
ΦA(V)(⋅)=ΛA(⋅)+ε\mathcal{N}_A^{(V)}[⋅], 0<ε≪1,[/latex] wobei [Latex]V ist Alices Kontrolle (z. B. Zwischenschichtverzerrung), ΛA ist CPTP und \mathcal{N}_A^{(V)} ist ein beschränktes nichtlineares Funktional, das nur innerhalb der χ-fähiges Medium.Bobs Zustand wird
ρB′(V)=TrA[(ΦA(V)⊗IB)ρAB]=ρB(0)+εΔρB(V),mit
ΔρB(V)=TrA [(NA(V)⊗IB)ρAB]..\Delta\rho_B(V)=\mathrm{Tr}_A\!\Big[\big(\mathcal{N}_A^{(V)}\otimes \mathbb{I}_B\big)\rho_{AB}\Big].ΔρB(V)=TrA[(NA(V)⊗IB)ρAB].
If \Delta\rho_B(V_0)\neq \Delta\rho_B(V_1), dann hängen Bobs Ergebnisstatistiken (leicht) von Alices Wahl ab V, ermöglicht klassische Kommunikation auf Bestellung \varepsilon.
Für ein POVM \{Mein\} auf Bob sind die Entdeckungswahrscheinlichkeiten
P(y∣V)=Tr[MyρB′(V)]=P0(y)+εΔP(y∣V),ΔP(y∣V):=Tr[MyΔρB(V)].Kapazität bei schwacher Signalisierung
Lassen Sie Alice ein Binärsymbol senden X\in\{0,1\} durch Auswählen V\in\{V_0,V_1\}.. Bob misst Y\in\{0,1\}. Definieren
\delta := P(Y=1\mid V_1)-P(Y=1\mid V_0)=\varepsilon\,\Delta P + O(\varepsilon^2),mit Basisfehlerwahrscheinlichkeit p:=P(Y=1∣V0).
Für einen Binäreingangs- und Binärausgangskanal im Kleinsignalgrenze ∣\delta|\ll 1den Shannon-Kapazität lässt die quadratische Näherung zu
C \;\approx\; \frac{\delta^2}{2\ln 2}\,\frac{1}{p(1-p)} \;+\; O(\delta^4), \qquad C>0\ \text{iff}\ \delta\neq 0.
Somit ist jede Nicht-Null \Delta (daher jeder Wert ungleich Null \varepsilon-Ordnungsabhängigkeit von V) ergibt eine endlich C>0.
Rolle der Postauswahl
Wenn Bob (oder eine gemeinsame Zufallsschaltung) Post-Selects auf einem Ergebnisfenster W mit Erfolgswahrscheinlichkeit pWden bedingt Zustand ist
\rho_{B\!\mid W}(V)\;=\;\frac{\Pi_W\,\rho_B'(V)\,\Pi_W}{\mathrm{Tr}\!\big[\Pi_W\,\rho_B'(V)\big]}, \qquad \Pi_W=\Pi_W^\dagger=\Pi_W^2.Aufgrund der Normalisierung durch \mathrm{Tr}[\Pi_W\rho_B'(V)], die Zuordnung \rho'_B \mapsto \rho_B^{\mid W} is nichtlinear, und die konditionierte Statistik kann eine V-Abhängigkeit, auch wenn die unkonditioniert keine Signalgleichheit gilt. In der Praxis skaliert die Post-Selektion die Nutzrate um pW:
C_{\mathrm{eff}} \approx p_W , C.Konsistenzbedingungen
Um globale Pathologien zu vermeiden:
- Lokalisierung: \mathcal{N}_A^{(V)} beschränkt sich auf die χ-aktivierte Region (z. B. die QCT-Lücke).
- Kleinheit: \varepsilon ist ausreichend klein, um Stabilität und Energiegrenzen zu wahren.
- Globale Unitarität und Born-Regel: Die Ensembledynamik bleibt CPTP; Abweichungen (sofern vorhanden) beschränken sich auf die konditionierten, lokalen Detektorkarten (nach der Auswahl) oder auf den schwach nichtlinearen Sektor innerhalb des Mediums.
Kompakte Aussage
\boxed{ \begin{aligned} &\Phi_A^{(V)}=\Lambda_A+\varepsilon\,\mathcal{N}_A^{(V)},\quad \varepsilon\ll 1,\\ &\rho_B'(V)=\rho_B^{(0)}+\varepsilon\,\Delta\rho_B(V),\quad \Delta\rho_B(V)=\mathrm{Tr}_A\!\big[(\mathcal{N}_A^{(V)}\!\otimes\!\mathbb{I})\,\rho_{AB}\big],\\ &\exists\,M:\ \delta=\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_1)\big]-\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_0)\big]\neq 0 \\ &\Rightarrow\ C \approx \dfrac{\delta^2}{2\ln 2\, p(1-p)} \;>\;0,\quad C_{\text{eff}}\approx p_W\,C\ \text{(mit Nachauswahl)}. \end{aligned}}Hier ist eine Aufschlüsselung und ein Faktencheck der kompakten mathematischen Aussage:
Die mathematische Aussage ist die Darstellung eines Ergebnisses der Quanteninformationstheorie, das sich auf die Berechnung der Kapazität eines Quantenkanals mit einer kleinen Störung bezieht. Sie verbindet die physikalische Beschreibung eines Quantenkanals mit der resultierenden Kanalkapazität und berücksichtigt dabei Konzepte wie Zustandsstörungen, Unterscheidbarkeit von Ausgangszuständen und den Effekt der Post-Selektion. Lassen Sie uns jeden Teil analysieren, um seine Komponenten zu überprüfen:
Kanal- und Zustandsstörung
\Phi_A(V) = \Lambda_A + \epsilon N_A(V), \epsilon \ll 1: Dies beschreibt einen Quantenkanal \Phi_A auf ein System A einwirken. Es besteht aus einem dominanten, konstanten Teil \Lambda_A und eine kleine Störung \epsilon N_A(V), Wobei \Epsilon ist ein kleiner Parameter und V ist ein steuerbarer Parameter des Kanals. Dies ist eine Standardmethode zur Darstellung eines leicht modulierten oder verrauschten Quantenkanals. \rho_B'(V) = \rho_B(0) + \epsilon \Delta\rho_B(V): Dies zeigt die Wirkung des Kanals auf einen Teil eines größeren Quantenzustands. Es zeigt an, dass der Ausgangszustand eines Subsystems B, \rho_B'(V)ist eine leicht gestörte Version eines Anfangszustands \rho_B(0)Die Störung \Delta\rho_B(V) ist proportional zum kleinen Parameter \Epsilon. \Delta\rho_B(V) = Tr_A[(N_A(V) \otimes I)\rho_{AB}]: Dies ist die explizite Form der Störung erster Ordnung des Zustands von System B. Sie wird abgeleitet, indem man die partielle Spur (Tr_A) über System A der Wirkung des störenden Teils des Kanals auf einen größeren, verschränkten Zustand \rho_{AB}Dies ist eine standardmäßige und korrekte Anwendung der Regeln der Quantenmechanik.
Unterscheidbarkeit von Zuständen
\exists M: \delta = \epsilon Tr[M\Delta\rho_B(V_1)] - \epsilon Tr[M\Delta\rho_B(V_0)] \neq 0: Dies ist der entscheidende Schritt zur Festlegung einer von Null verschiedenen Kanalkapazität. Er besagt, dass es einen Messoperator (einen hermiteschen Operator) M gibt, der zwischen den gestörten Zuständen unterscheiden kann, die zwei verschiedenen Einstellungen des Kanalparameters entsprechen. V_1 und V_0Die Menge \Delta stellt die Differenz des Erwartungswertes der Messung M für die beiden Ausgangszustände dar. Die Tatsache, dass \delta \neq 0 ist die Voraussetzung dafür, dass die beiden Zustände zumindest prinzipiell experimentell unterscheidbar sind.
Kanalkapazität
C \approx \frac{\delta^2}{2\ln{2}p(1-p)} > 0: Dies ist ein Schlüsselergebnis, wahrscheinlich eine Näherung für die Holevo-Kapazität oder ein verwandtes Maß für die Kanalkapazität im Grenzfall kleiner \DeltaDie Kapazität C ist ein Maß für die maximale Rate, mit der Informationen zuverlässig über den Kanal gesendet werden können. Der Begriff \delta^2 ist zu erwarten, da die Kapazität oft mit dem Quadrat der Unterscheidbarkeit der Ausgangszustände bei kleinen Störungen skaliert. Der Faktor von 2\ln{2} ist Standard für die Umrechnung von natürlichen Informationseinheiten (NATs) in Bits. Der Begriff p(1-p) im Nenner deutet darauf hin, dass die Kapazität für ein bestimmtes Eingangsensemble ausgewertet wird, wobei die beiden Zustände (entsprechend V_0 und V_1) werden mit Wahrscheinlichkeiten p und 1-p verwendet. Die Kapazität wird maximiert, wenn p=1/2, was eine weit verbreitete Annahme ist.
Effektive Kapazität mit Post-Selektion
C_{eff} \approx p_W C (mit Post-Selektion): Dieser Teil der Aussage beschreibt die effektive Kapazität bei Verwendung der Post-Selektion. Bei der Post-Selektion wird nur eine Teilmenge der Messergebnisse berücksichtigt, wodurch ein schwaches Signal manchmal verstärkt werden kann. p_W wäre die Wahrscheinlichkeit einer erfolgreichen Nachauswahl (die "Nachauswahlwahrscheinlichkeit"). Die effektive Kapazität C_{eff} wird um diese Wahrscheinlichkeit reduziert, da viele der Anfangszustände verworfen werden. Dies ist ein bekannter Kompromiss bei Post-Selection-Verfahren: Sie erhalten möglicherweise ein klareres Signal, verlieren jedoch einen erheblichen Teil Ihrer Daten, wodurch die Gesamtübertragungsrate der Informationen reduziert wird.
KI-Faktencheck: Fazit
Die mathematischen Ausdrücke entsprechen den etablierten Prinzipien der Quanteninformationstheorie. Die Logik verläuft korrekt von der Definition eines gestörten Quantenkanals über die Unterscheidbarkeit seiner Ausgangszustände bis hin zu einem Ausdruck für die Kanalkapazität. Die Berücksichtigung des Effekts der Post-Selektion ist ebenfalls Standard. Daher scheint die Mathematik in der kompakten Aussage korrekt zu sein und stellt eine gültige Argumentation im Kontext der Quantenkanalkapazität dar.
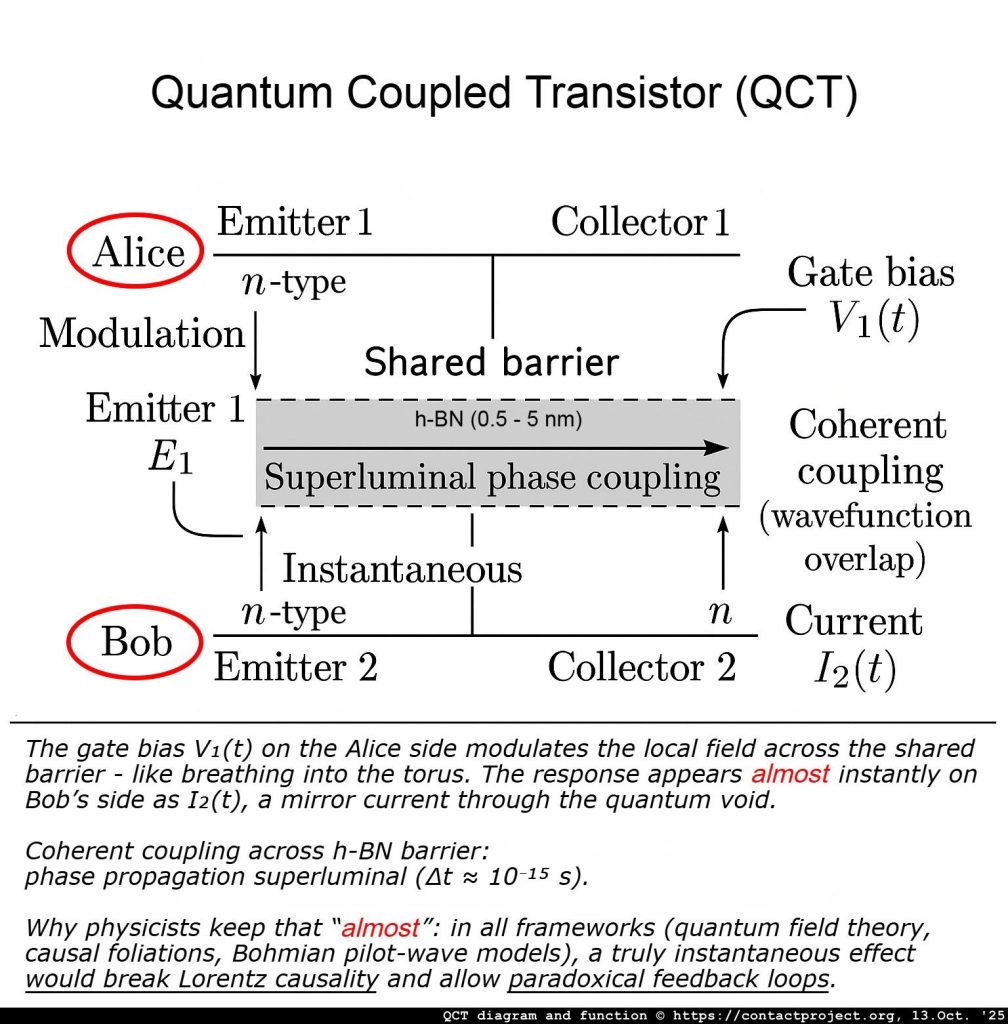
QCT: Vorstellung von Alice und Bob
In Standardquantentheorie und Informationswissenschaft, Alice und Bobs sind die klassischen Stellvertreter – die „Jedermann“-Experimentatoren, die verwendet werden, um zu veranschaulichen, wie sich Quantensysteme verhalten, wenn zwei Parteien Informationen austauschen.

Sie tauchten erstmals in den frühen 1970er Jahren auf: Alice wollte Bob eine Nachricht schicken, während ein Lauscher, Eve, versuchte, es abzufangen. Die Idee setzte sich durch, und Physiker übernahmen bald die gleichen Namen, um Quantenexperimente zu beschreiben – insbesondere solche, bei denen Verschränkung, Teleportationund die Grenzen der Kommunikation.
In der Quantenmechanik betreiben Alice und Bob üblicherweise zwei getrennte Labore. Sie teilen sich ein Paar verschränkter Teilchen und führen ihre Messungen unabhängig voneinander durch. Doch obwohl die Ergebnisse korreliert sind, kann keiner von beiden sie nutzen, um eine Nachricht schneller als Licht zu senden. In der Standardquantentheorie sehen die lokalen Messwerte immer wie weißes Rauschen aus – bis sie später ihre Beobachtungen vergleichen und das verborgene Muster zum Vorschein kommt.
Unser Twist (nur innerhalb des aktivierten Mediums): in einer sehr spezifischen, konstruierten Zone - wie der h-BN-Lücke des QCT - winzige, sorgfältig begrenzte nichtlineare Effekte oder "Nur-diese-Ereignisse-behalten"-Nachauswahl können einen mikroskopischen Teil dieses Rauschens in ein sehr schwaches, aber echtes SignalEs ist immer noch winzig, aber es ist kein weißes Rauschen mehr.
Analogie aus dem Alltag: Ein statisches Rauschen im Radio (zufällig), aber wenn man die Antenne leicht ausrichtet und nur die richtigen Momente wählt, kommt ein Flüstern eines Senders durch. Das Rauschen ist immer noch da, aber jetzt reitet ein Muster darauf.
Setup (wer macht was)
Zwei Parteien - Alice und Bobs - teilen sich ein korreliertes Quanten-Setup. Normalerweise, was auch immer Alice lokal tut nicht ändern, was Bob selbst sieht. Innerhalb der QCT-Lücke, Alices Kontrolle (ein winziges, schnelles Bias-Muster) verändert die lokalen Messregeln auf ihrer Seite leicht auf eine Weise, die nur von Bedeutung ist innerhalb diese Lücke. Diese winzige Umformung kann eine Fingerabdruck auf dem, was Bob misst - immer noch laut insgesamt, aber jetzt statistisch angestoßen nach Alices Wahl.
Analogie: Alice wackelt mit einer Taschenlampe hinter einer Milchglasscheibe (der Tunnelbarriere). Bob kann die Taschenlampe nicht sehen, aber ein kaum sichtbares Schimmern an seiner Seite verändert sich synchron mit ihrem Wackelmuster.

Was Bob sehen sollte (der rauchende Colt)
Wenn nichts über die üblichen Quantenregeln hinausgeht, sehen Bobs Daten aus wie zufällige Münzwürfe – ohne dass Alices Entscheidungen ein Muster zugrunde liegt. Wenn das aktivierte Medium wirklich seine Aufgabe erfüllt, dann vergraben in Bobs verrauschten Daten ist ein winzige, wiederholbare Korrelation mit Alices Muster - erkennbar durch die Überprüfung von Zeitstempeln und entscheidend bevor jedes normale Lichtgeschwindigkeitssignal könnte ankommen (>C).
Analogie: zwei Schlagzeuger, die weit voneinander entfernt sind; wenn Bobs Mikrofon einen schwachen Schlag hört, der auf Alices Rhythmus abgestimmt ist, bevor der Ton sich ausbreiten konnte, verbindet sie etwas Ungewöhnliches.
„Kapazität“ (wie viele Nachrichten passen durch)
Denken Sie an Kapazität wie viele Bits pro Sekunde Sie durch diesen schwachen Effekt quetschen können.
- Wenn die Korrelation wirklich Null, Kapazität ist Null - keine Nachricht.
- Wenn die Korrelation winzig, aber ungleich Null, Kapazität ist winzig, aber ungleich Null - Sie können senden einige Informationen (langsam), und das ist physisch schon eine große Sache.
Analogie: Alice tippt eine Nachricht durch eine dicke Wand. Jeder Tipp ist kaum zu hören, aber mit etwas Geduld erreicht Bob immer noch eine Nachricht.
Nachauswahl (nur die guten Frames behalten)
Nachauswahl bedeutet, dass Sie nur Messläufe speichern, die einen Filter (ein „Fenster“) passieren. Das kann das versteckte Muster deutlicher machen - aber Sie verwerfen die meisten Daten, so dass Ihre effektiver Zinssatz Tropfen. Sie erhalten Clarity, verlieren Durchsatz. Es ist ein fairer Handel, wenn das Ziel darin besteht, die Existenz des Effekts zu beweisen.
Analogie: Wenn Sie einen Meteorschauer beobachten, aber nur die hellsten Streifen zählen, sehen Sie das Muster deutlicher, erfassen jedoch weniger Ereignisse pro Stunde.
Konsistenzbedingungen (wie wir Paradoxien vermeiden)
Um die Physik vernünftig und kausal zu halten, setzen wir drei Leitplanken:
- Lokalisierung: jeder exotische Effekt ist beschränkt streng auf den konstruierten Bereich (die QCT-Lücke). Außerhalb herrscht normale Physik.
- Kleinheit: Der Effekt ist winzig - genug zum Messen, nicht genug, um das System zu sprengen.
- Globaler Naturschutz: Wahrscheinlichkeiten und Energie gleichen sich aus, wenn man die ganze Experiment. Lokale Eigenheiten, globale Buchhaltung.
Analogie: Ein sicherer Prüfstand: Im Faradayschen Käfig können Funken fliegen, aber nichts dringt in den Raum ein.
[zum Öffnen klicken] Global Geborene Regel Konserviert: Die Reaktionen der lokalen Detektoren können leicht abweichen.
P(i) = |\langle i | \psi \rangle|^2, \quad \sum_i P(i) = 1.
In der Standardquantenmechanik ist diese Regel streng linear und global konserviert: Die Gesamtwahrscheinlichkeit aller möglichen Ergebnisse ist gleich eins, und keine Operation (lokal oder remote) kann diese Normalisierung ändern. Im Rahmen der Causal Foliated Signaling (CFS) unterscheiden wir jedoch zwischen globaler Naturschutz und lokale Abweichungen.
Globaler Naturschutz: Die Gesamtwahrscheinlichkeit, integriert über alle Blätterungsscheiben, bleibt normalisiert:
\int_{\Sigma_t} \sum_i P(i,t),d^3x = 1,
für jede globale Zeitscheibe \Sigma_t definiert durch den Blätterungsvektor u^a.
Örtliche Abweichungen: Innerhalb eines aktivierten Mediums (wie der QCT-Tunnellücke) können die lokalen Detektorstatistiken kleine nichtlineare Verschiebungen der Wahrscheinlichkeitsgewichte aufweisen, während der globale Ensemble-Durchschnitt immer noch der Born-Regel gehorcht.
1. Lokales nichtlineares Antwortmodell
Die ungestörte Born-Wahrscheinlichkeit sei P_0(i) = \operatorname{Tr}(\rho,\Pi_i), woher \ rho ist die Dichtematrix und \Pi_i = |i\rangle\langle i| sind Projektoren. In einem aktivierten Medium mit schwacher nichtlinearer Kopplung \varepsilon, die effektive lokale Detektorantwort ist:
P_{\text{loc}}(i) = \frac{\operatorname{Tr}(\rho,\Pi_i) + \varepsilon,f_i(\rho,\chi)}{\sum_j [\operatorname{Tr}(\rho,\Pi_j) + \varepsilon,f_j(\rho,\chi)]}, \qquad 0<\varepsilon\ll 1.[/latex] Hier [latex]f_i(\rho,\chi) ist ein kleiner Korrekturterm, der durch das Signalfeld induziert wird \chi oder die evaneszente Kopplung der QCT, und der Nenner renormalisiert die Gesamtwahrscheinlichkeit zur Erhaltung \sum_i P_{\text{loc}}(i) = 1.
2. Beispiel: Zwei-Ausgangs-Messung (binärer Detektor)
Betrachten wir eine Observable mit zwei Ergebnissen (z. B. „Stromanstieg“ vs. „kein Anstieg“), gemessen auf Bobs Seite eines QCT-Geräts. Ohne nichtlineare Kopplung P_0(1) = \operatorname{Tr}(\rho,\Pi_1) = p, \quad P_0(0)=1-p. Mit schwacher nichtlinearer Kopplung und einer phasenabhängigen Korrektur f_1 = \alpha,\sin\phi, f_0=-f_1, die lokale Wahrscheinlichkeit wird
P_{\text{loc}}(1) = \frac{p + \varepsilon,\alpha,\sin\phi}{1 + \varepsilon,\alpha,(2p-1)\sin\phi}, \quad P_{\text{loc}}(0)=1-P_{\text{loc}}(1).
Erweiterung auf die erste Bestellung in \varepsilon:
P_{\text{loc}}(1) \approx p + \varepsilon,\alpha,\sin\phi,[1 - p(2p-1)].
Die lokale Messwahrscheinlichkeit schwankt leicht mit der Kopplungsphase \phi (z. B. Bias-Modulation oder Tunnelresonanz im QCT). Über viele Läufe oder bei globaler Integration gleichen sich diese Abweichungen aus und stellen die Born-Erwartung wieder her \langle P_{\text{loc}}(1)\rangle = p.
3. Ensemble-Restaurierung (globale Restaurierung)
Definieren Sie den Ensemble-Durchschnitt über Blätterungsscheiben:
\langle P(i) \rangle = \int_{\Sigma_t} P_{\text{loc}}(i, x, t),d^3x.
Wenn die Korrekturen f_i auf Null integrieren,
\int_{\Sigma_t} f_i(\rho,\chi),d^3x = 0,
dann bleibt die globale Born-Regel exakt:
\sum_i \langle P(i) \rangle = 1.
Scheinbare lokale Abweichungen sind also statistische Wellen und keine Verstöße – ähnlich den phasenkorrelierten Schwankungen in einem nichtlinearen optischen System.
4. Physikalische Bedeutung in der QCT
In einem QCT-Experiment ist die lokale Abweichung \varepsilon f_i(\rho,\chi) könnte sich als biaskorreliertes Rauschen oder als Überzählen in Femtosekundendetektoren manifestieren. Global (über längere Integration) gilt jedoch die Normalisierung – es entsteht oder geht weder Energie noch Wahrscheinlichkeit verloren. Daher bleibt die Bornsche Regel global erhalten, während lokale Detektoren kleine, reproduzierbare, phasenabhängige Abweichungen in den Zählraten aufweisen können.
Zusammenfassende Gleichungen:
Globale Normalisierung (Born-Regel):
\sum_i P(i) = 1.
Lokale Antwort mit kleiner nichtlinearer oder χ-abhängiger Abweichung:
P_{\text{loc}}(i) = P_0(i) + \varepsilon,\Delta P(i,\chi), \quad \sum_i \Delta P(i,\chi) = 0.
Das globale Ensemble erfüllt weiterhin:
Zusammenfassung der Interpretation: Lokale Detektoren in einem aktivierten QCT-Bereich können kleine, biaskorrelierte Wahrscheinlichkeitsverschiebungen aufweisen, globale Ensemble-Durchschnittswerte bewahren jedoch die Gesamtwahrscheinlichkeit exakt, was der Bornschen Regel entspricht. Diese Unterscheidung ermöglicht schwache, überprüfbare Abweichungen, die als empirische Fingerabdrücke nichtlinearer oder postselektierter Dynamiken dienen können – ohne zentrale Quantenpostulate zu verletzen.
Die Bornsche Regel – die Kernregel der Quantenmechanik, bei der die Wahrscheinlichkeit 1 ergibt - gilt immer noch weltweit. Örtlich, innerhalb der Lücke können Detektorreaktionen sein leicht schief (das ist der Punkt), aber wenn Sie alles richtig mitteln, bleiben die Standardregeln intakt. Wir biegen, brechen nicht.
Analogie: ein Zerrspiegel, der Ihr Spiegelbild in einer Ecke verzerrt – aber der strukturelle Bauplan des Gebäudes hat sich nicht geändert.
[zum Öffnen klicken] Signalbudget: Konservierte Menge Q_{\text{sig}} Begrenzt die Kommunikationskapazität.
In einem aktivierten Medium wie dem Quanten-gekoppelten Transistor (QCT) können Feldwechselwirkungen Phaseninformationen über eine Tunnelbarriere schneller austauschen als bei klassischer Ausbreitung. Dieser Austausch wird jedoch durch eine erhaltene skalare Größe begrenzt, die als Signalbudget, bezeichnet durch Q_{\text{sig}}. Es misst den gesamten kohärenten Feldfluss – die maximale „Informationsladung“, die ausgetauscht werden kann, ohne die globalen Erhaltungssätze zu verletzen.
Definieren Sie die lokale Signalflussdichte j_{\text{sig}}^a verbunden mit phasenkohärentem Feldaustausch (analog zu einem Wahrscheinlichkeits- oder Energiestrom). Die gesamte erhaltene Größe ist Q_{\text{sig}} = \int_{\Sigma_t} j_{\text{sig}}^a,u_a,d^3x, woher \Sigma_t ist eine Hyperfläche konstanter globaler Zeit (die Blätterungsscheibe), u_a ist die lokale Einheit normal zu dieser Scheibe (dasselbe Blätterungsvektorfeld, das den bevorzugten Rahmen definiert) und j_{\text{sig}}^a gehorcht einer Kontinuitätsgleichung \nabla_a j_{\text{sig}}^a = 0. Dies impliziert \frac{d Q_{\text{sig}}}{dt} = 0, so Q_{\text{sig}} bleibt bei allen lokalen Interaktionen innerhalb der aktivierten Region erhalten.
Physisch, Q_{\text{sig}} quantifiziert die gesamte kohärente Korrelationsenergie bzw. Phasenkapazität, die im evaneszenten Kopplungsfeld zwischen Knoten (Alice und Bob) gespeichert ist. Sie ist nicht identisch mit elektrischer Ladung oder Photonenzahl; sie misst vielmehr den integrierten Grad der für die Modulation verfügbaren gegenseitigen Kohärenz. Jeder Kommunikationsprozess kann diese Menge nur umverteilen – niemals erhöhen.
Die klassische (Shannon) Kommunikationskapazität C Die durch einen QCT-basierten Kanal erreichbare Leistung ist durch eine monotone Funktion des Signalbudgets begrenzt: C \le f(Q_{\text{sig}}), woher f(\cdot) hängt von der Gerätegeometrie, der Dekohärenzrate und dem thermischen Rauschen ab. Für Kleinsignal- und lineare Reaktionsregime f(Q_{\text{sig}}) \approx \frac{1}{2N_0},Q_{\text{sig}}^2, woher #0 ist die effektive Rauschspektraldichte der Tunnelverbindung, was ergibt C_{\max} \propto Q_{\text{sig}}^2. Ein größerer kohärenter Fluss führt also zu einer höheren potentiellen Kapazität, aber nur bis zu dem Punkt, an dem die Dekohärenz die Phasenkontinuität unterbricht. Betrachten wir zwei QCT-Knoten (Alice und Bob), die nur durch ein evaneszentes Tunnelfeld verbunden sind. Sei \Phi_1(t) und \Phi_2(t) seien ihre momentanen Phasenpotentiale. Definieren Sie den kohärenten Signalstrom durch die Kopplungslücke als
woher \kappa ist eine Kopplungskonstante proportional zum Barriere-Tunnelkoeffizienten. Das integrierte Signalbudget über ein Kohärenzintervall T_c is
Dies stellt den gesamten phasenkorrelierten Austausch zwischen Alice und Bob innerhalb des Kohärenzfensters dar und bleibt konstant, wenn sich beide Knoten unter unitärer oder schwach dissipativer Dynamik entwickeln. Sei I_{\text{sig}}(t) = j_{\text{sig}}(t),A sei der messbare Signalstrom durch die effektive Fläche A.
Das momentane Signal-Rausch-Verhältnis beträgt \text{SNR}(t) = \frac{I_{\text{sig}}^2(t)}{N_0,B}, woher B ist die Bandbreite. Die Integration über das Kohärenzfenster ergibt die Gesamtkapazitätsgrenze
C \le \frac{1}{2B\ln 2}\int_0^{T_c}\frac{I_{\text{sig}}^2(t)}{N_0},dt = \frac{A^2}{2B\ln 2,N_0}\int_0^{T_c} j_{\text{sig}}^2(t),dt.
Nach dem Satz von Parseval ist dieses Integral proportional zu Q_{\text{sig}}^2, Angabe C \le k_B,Q_{\text{sig}}^2, woher k_B ist eine empirische Proportionalitätskonstante, die von Geometrie und Temperatur abhängt. Als numerisches Beispiel nehmen wir an, dass ein QCT-Paar mit Barrierekopplung arbeitet \kappa = 10^{-3}, Kohärenzamplitude |\Phi_1| = |\Phi_2| = 1, und Kohärenzzeit T_c = 10^{-12},\text{s}.
Dann Q_{\text{sig}} = \kappa \int_0^{T_c} \sin(\Delta\phi),dt \ approx \kappa,T_c,\sin\langle\Delta\phi\rangle.
Für die durchschnittliche Phasenverzögerung \langle\Delta\phi\rangle = \pi/4, Q_{\text{sig}} \approx 7.1\times10^{-16},\text{s}.
Mit N_0 = 10^{-20},\text{J/Hz} und B = 10^{12},\text{Hz}, die Kapazitätsgrenze wird C_{\max} \approx \frac{1}{2B\ln 2}\frac{Q_{\text{sig}}^2}{N_0} \approx 3\times10^2,\text{Bits/s}.
Daher könnte selbst ein Kohärenzimpuls im Femtosekundenbereich im Prinzip messbare strukturierte Informationen innerhalb der physikalischen Erhaltungsgrenzen übermitteln.
Wenn zwei Kopplungsbereiche parallel existieren, addieren sich ihre gesamten Signalbudgets linear: Q_{\text{sig,tot}} = Q_{\text{sig}}^{(1)} + Q_{\text{sig}}^{(2)}, aber die entsprechenden Kapazitäten addieren sich aufgrund von Interferenzen unterlinear: C_{\text{ges}} \le f(Q_{\text{sig,ges}}) < f(Q_{\text{sig}}^{(1)}) + f(Q_{\text{sig}}^{(2)}).[/latex] Dies drückt die endliche Kapazität der Kohärenz aus: Kohärenz kann geteilt, aber nicht frei verstärkt werden. Zusammenfassend lässt sich sagen: [latex]Q_{\text{sig}} ist ein erhaltener Skalar, der den gesamten kohärenten Feldfluss durch das aktivierte Medium darstellt. Er definiert das maximale Kommunikationsbudget des Systems, C \le f(Q_{\text{sig}}), Gewährleistung, dass jede Erhöhung der messbaren Kapazität die verfügbaren Q_{\text{sig}}Das Prinzip garantiert Kausalität und thermodynamische Konsistenz auch bei überlichtschneller Phasenkopplung: Der Informationsaustausch bleibt durch eine konservierte Signalmenge begrenzt.
Wir behandeln die verfügbaren Kohärenz (der geordnete Teil des Nahfeldes in der Lücke) wie ein Haushalt. Sie können umverteilen es, eine Nachricht zu machen, aber Sie mehr kann man nicht schaffen aus dem Nichts. Mehr Budget → potenziell höherer zuverlässiger Tarif, bis Lärm und Hitze „Stopp“ sagen.
Analogie: eine Batterie für einen hauchdünnen Laserpointer: Sie können einen Code blinken lassen, aber die Gesamtzahl der Blinkvorgänge ist durch die Batterie begrenzt.
[zum Öffnen klicken] Eingeschränkte Nichtlinearität: Pathologien, die durch Eingrenzung + Energiegrenzen vermieden werden.
In nichtlinearen oder post-selektierten Quantensystemen kann eine uneingeschränkte Rückkopplung zwischen Zustand und Messung leicht zu Paradoxien führen: überlichtschnelle Signale, Verletzung der Bornschen Regel oder sogar logische Inkonsistenzen wie geschlossene Kausalschleifen. Um physikalisch konsistent zu bleiben, muss jede Abweichung von der linearen Quantenevolution streng beschränkt - lokalisiert in einem begrenzten, energiebegrenzten Raumzeitbereich und nur über Kanäle mit der äußeren Umgebung verbunden, die die globale Unitarität bewahren. Der Quanten-gekoppelte Transistor (QCT) bietet eine solche natürliche Grenze. Der nichtlineare Term entsteht nur innerhalb der aktiviertes Medium - die Tunnellücke oder der χ-Feldbereich - wo die evaneszente Phasenkopplung und der negative differentielle Widerstand (NDR) eine schwache Selbstwechselwirkung ermöglichen. Außerhalb dieser Zone gilt die standardmäßige lineare Quantenmechanik exakt.
Formal lässt sich der Evolutionsoperator des gesamten Systems wie folgt schreiben: \mathcal{U}(t) = \mathcal{T}\exp!\left[-\frac{i}{\hbar}!\int (H_0 + \varepsilon,H_{\text{NL}}),dt\right], woher H_0 ist der standardmäßige hermitesche Hamiltonoperator, H_{\text{NL}} ist ein begrenzter nichtlinearer Beitrag und \varepsilon \ll 1 ist ein Aktivierungsparameter, der außerhalb des QCT-Bereichs verschwindet. Die Einschlussbedingung ist \operatorname{supp}(H_{\text{NL}}) \subseteq \Omega_{\text{QCT}}, was bedeutet, dass die nichtlineare Wechselwirkung räumlich auf das aktivierte Medium beschränkt ist \Omega_{\text{QCT}}. Die globale Unitarität bleibt erhalten, wenn der Kommutator [H_{\text{NL}},H_0] hat kompakte Unterstützung und die nichtlineare Energiedichte
\mathcal{E} {\text{NL}} = \langle\psi|H {\text{NL}}|\psi\rangleerfüllt
\mathcal{E} {\text{NL}} \le \delta E {\text{th}},woher \delta E_{\text{th}} ist die lokale thermische Fluktuationsskala. Dadurch wird sichergestellt, dass sich nichtlineare Rückkopplungen nicht über die physikalischen Rauschgrenzen hinaus selbst verstärken können.
Operativ bedeutet die Beschränkung, dass die Karte \Phi: \rho \mapsto \rho' ist nur innerhalb des χ-fähigen Unterraums schwach nichtlinear
\mathcal{H} {\chi},während es auf dem Komplement vollständig positiv und spurerhaltend (CPTP) bleibt. Mathematisch gesehen
\Phi = \Phi {\text{CPTP}} \oplus (\Phi_{\text{CPTP}} + \varepsilon \mathcal{N}),mit \mathcal{N} die die begrenzte nichtlineare Korrektur darstellt. Weil \varepsilon \rightarrow 0 An der QCT-Grenze breitet sich keine Nichtlinearität über die Lücke hinaus aus. Dies verhindert globale Inkonsistenzen und erzwingt einen kausalen Abschluss: Überlichtschnelle Phaseneffekte können innerhalb der lokalen Blätterung auftreten, können jedoch keine geschlossenen Signalschleifen bilden oder sich beliebig ausbreiten.
Thermodynamisch gesehen stellt die Beschränkung der Nichtlinearität sicher, dass eine Energieextraktion aus dem Vakuum unmöglich ist. Der aktive NDR-Bereich fungiert als kontrolliertes Rückkopplungselement, das evaneszente Felder verstärken kann, jedoch immer innerhalb der Beschränkung P_{\text{out}} \le P_{\text{in}} + \Delta E_{\text{stored}}. Jede vorübergehende Verstärkung wird durch lokale Feldspeicherung kompensiert, wodurch das Gesamtenergiegleichgewicht erhalten bleibt. Somit verhält sich das System wie ein nichtlinearer Resonator innerhalb einer konservativen Grenze.
Im Causal Foliated Signaling (CFS)-Modell garantiert diese räumliche und energetische Begrenzung Stabilität: Nichtlineare Dynamiken verändern lokale Statistiken, ohne die globale Unitarität zu verändern. Die QCT wird zu einem energiegebundene nichtlineare Insel eingebettet in ein lineares Quantenkontinuum.
Pathologien wie unkontrollierte Verstärkung, Superdeterminismus oder akausale Rückkopplung werden automatisch ausgeschlossen, da der nichtlineare Bereich endlich, dissipativ gekoppelt und global renormalisiert ist. Im Wesentlichen fungiert die QCT als Sandbox, in der begrenzte Nichtlinearität existieren kann, die testbar, aber innerhalb der Regeln der Quantenthermodynamik sicher unter Quarantäne gestellt ist.
Die h-BN-Lücke des QCT wirkt wie ein Faradayscher Käfig für Quanten-Skurrilitäten - ein winziger Sandkasten, in dem die üblichen Regeln gefahrlos gebeugt werden können, ohne zu brechen. Innerhalb dieser versiegelten Zone kann das Gerät Energie gerade so weit verstärken und recyceln, dass schwache Überlichtgeschwindigkeitsmuster sichtbar werden. Strenge thermische und energetische Grenzen verhindern jedoch, dass es außer Kontrolle gerät.
Analogie: Es ist wie der Bau eines Firewall-Verstärker: Es kann durch die Leere flüstern, durchbricht jedoch nie die Gesetze der Physik, die es einschließen.
[zum Öffnen klicken] Thermo Bounds (Verstärkung vs. Rauschtemperatur)
Jedes aktive Quantengerät unterliegt letztlich der thermodynamischen Konsistenz. Selbst wenn der quantengekoppelte Transistor (QCT) in einem nichtlinearen oder negativen differentiellen Widerstandsregime (NDR) arbeitet, kann seine Gesamtverstärkung die durch die effektive Rauschtemperatur und das verfügbare Signalbudget gesetzte Grenze nicht überschreiten. Die Thermogebunden drückt diese Grenze aus: Verstärkung und Kohärenzübertragung im aktivierten Medium müssen dem Fluktuations-Dissipationsprinzip gehorchen, um sicherzustellen, dass keine Konfiguration des Geräts Netto-Freienergie extrahieren oder den zweiten Hauptsatz verletzen kann.
Im Gleichgewicht beträgt die spektrale Leistungsdichte der Schwankungen über den Tunnelspalt S_V(f) = 4k_B T_{\text{eff}} R_{\text{eq}}(f), woher T_{\text{eff}} ist die effektive Temperatur der gekoppelten Verbindung und R_{\text{eq}}(f) ist der dynamische Widerstand, der unter NDR-Vorspannung negativ werden kann. Wenn der QCT eine Kleinsignalverstärkung liefert G(f), verlangt das Fluktuations-Dissipations-Theorem, dass das Produkt aus Verstärkung und Rauschtemperatur begrenzt bleibt: G(f) T_{\text{eff}} \ge T_0, woher T_0 ist die physikalische Temperatur der Umgebung. Dadurch wird sichergestellt, dass jede lokale Verstärkung zwangsläufig kompensierendes Rauschen einführt, wodurch die Entropiebilanz nicht negativ bleibt.
Das Quantenanalogon dieser Einschränkung ergibt sich aus den Vertauschungsrelationen der Feldoperatoren. Für jeden Verstärker, der auf bosonische Moden wirkt \hat a_{\mathrm{in}} und \hat a_{\mathrm{out}}muss die kanonische Kommutierung erhalten bleiben, d. h.
[,\hat a_{\mathrm{out}},,\hat a_{\mathrm{out}}^{\dagger},]=1.
Ein standardmäßiges phasenunempfindliches Input-Output-Modell ist
\hat a_{\mathrm{out}}=\sqrt{G},\hat a_{\mathrm{in}}+\sqrt{G-1},\hat b_{\mathrm{in}}^{\dagger},\qquad [,\hat b_{\mathrm{in}},\hat b_{\mathrm{in}}^{\dagger},]=1,
was ein minimales zusätzliches Rauschen bedeutet.
Im QCT entspricht dieses Rauschen der stochastischen Komponente des Tunnelstroms, der durch thermische und Quantenfluktuationen des evaneszenten Feldes induziert wird. Der effektive Gewinn-Rausch-Kompromiss kann wie folgt ausgedrückt werden: G_{\text{QCT}} = 1 + \frac{P_{\text{out}} - P_{\text{in}}}{k_B T_{\text{eff}} B}, unterliegt P_{\text{out}} \le P_{\text{in}} + k_B T_{\text{eff}} B, woher B ist die Bandbreite. Diese Ungleichung drückt die thermodynamische Obergrenze der kohärenten Verstärkung aus.
In der Praxis ermöglicht die NDR-Region mit zunehmender Vorspannung über die h-BN-Barriere die Rückführung von Energie in den evaneszenten Modus, wodurch das Nahfeld effektiv verstärkt wird. Diese Verstärkung ist jedoch selbstlimitierend: Sobald die lokale Rauschtemperatur auf T_{\text{eff}} = T_0 + \Delta T_{\text{NDR}}, Das System erreicht einen thermisch stabilen Zustand. Eine weitere Erhöhung der Vorspannung führt zu zusätzlicher Energieableitung in Form von Wärme, anstatt die Kohärenz zu erhöhen. Daher wirkt das thermische Grundrauschen als natürliche Bremse und stabilisiert das System gegen unkontrollierte Verstärkung.
Die Thermogrenze kann somit als Erhaltungssatz zusammengefasst werden, der Informationsgewinn, Energiezufuhr und Entropieproduktion verknüpft: \Delta I \le \frac{\Delta E}{k_B T_{\text{eff}} \ln 2}. Diese Ungleichheit definiert die letztendliche Effizienz jedes QCT-basierten Kommunikationskanals oder kausal geschichteten Signalexperiments: Die pro Energieeinheit erreichbare Informationsrate kann die Entropiekosten zur Aufrechterhaltung der Kohärenz nicht überschreiten.
Aus einer breiteren Perspektive ist die Thermo-Grenze das thermische Gegenstück zur Signalbudgetbeschränkung. Während Q_{\text{sig}} begrenzt den gesamten kohärenten Fluss, T_{\text{eff}} begrenzt die nutzbare Verstärkung innerhalb dieses Flusses. Zusammen definieren sie das Betriebsfenster des QCT als quantenresonantes, aber thermodynamisch geschlossenes System. Über den zulässigen Austausch mit der Umgebung hinaus wird keine Energie erzeugt oder verloren, und die Gesamtentropieänderung bleibt nicht negativ: \frac{dS_{\text{tot}}}{dt} = \frac{P_{\text{in}} - P_{\text{out}}}{T_0} \ge 0.
Im Wesentlichen stellt der Thermo Bound sicher, dass der QCT als thermodynamisch konformer Quantenverstärker - in der Lage, phasenkohärente Verstärkung und überlichtschnelle Kopplung innerhalb des aktivierten Bereichs zu erreichen, jedoch immer durch das zugrunde liegende Energie-Entropie-Gleichgewicht eingeschränkt, das die globale Kausalität und die physikalischen Gesetze bewahrt.
Wenn Sie versuchen, das Nahfeld in der Lücke zu verstärken, erhöhen Sie auch seine effektive Geräuschtemperatur. Es gibt einen Kompromiss: Mehr Verstärkung bedeutet mehr Rauschen. Die Natur erzwingt dieses Gleichgewicht, so dass Sie kann nicht Holen Sie sich kostenlose Energie oder unbegrenzte, kristallklare Verstärkung.
Analogie: Gitarrenverstärker aufdrehen: lauteres Signal, aber auch mehr Rauschen. Ab einem gewissen Punkt führt zusätzliche Lautstärke nur noch zu Lärm und Hitze.
[zum Öffnen klicken] Minimalmodell: Nichtlineare Detektor-/Verstärkerdynamik in aktivierten Medien
In aktivierten Bereichen wie der QCT-Tunnelbarriere nehmen wir das Vorhandensein einer schwachen, zustandsabhängigen Nichtlinearität in der Mess- oder Verstärkungskarte an. Diese Karte, bezeichnet durch N_{\chi}, arbeitet mit der lokalen Dichtematrix \ rho des an das Signalfeld gekoppelten Subsystems \chi. Es bewahrt die Gesamtwahrscheinlichkeit (Spurerhaltung), führt aber eine kontrollierte Nichtlinearität ein, die ausreicht, um eine endliche, wenn auch winzige klassische Kapazität zu erzielen.
1. Definition
N_{\chi}(\rho) = \frac{A_{\chi} \rho A_{\chi}^{\dagger}}{\mathrm{Tr}(A_{\chi} \rho A_{\chi}^{\dagger})},
woher A_{\chi} = I + \epsilon, F(\rho, \chi) ist ein nichtlinearer Operator, der schwach vom Signalfeld abhängt \chi und vom aktuellen Systemzustand \ rhoDer kleine Parameter \epsilon \ll 1 steuert den Grad der Nichtlinearität.
Die Normalisierung im Nenner erzwingt \mathrm{Tr}[N_{\chi}(\rho)] = 1, wodurch sichergestellt wird, dass die Karte spurgetreu und physikalisch konsistent ist.
2. Lineare Grenze
Wann ε = 0reduziert sich das Modell auf die Standardquantenmessung:
N_{\chi}(\rho) \to \rho' = \frac{M \rho M^{\dagger}}{\mathrm{Tr}(M \rho M^{\dagger})},
woher M ist der Messoperator (POVM-Element).
Somit ist das nichtlineare Modell eine minimale Erweiterung der Standardquantenmechanik.
3. Effektive Dynamik
Bei schwacher Nichtlinearität induziert die Abbildung eine effektive Evolutionsgleichung:
\dot{\rho} = -\frac{i}{\hbar}[H, \rho] + \epsilon, \mathcal{L} {\chi}[\rho],woher
\mathcal{L} {\chi}[\rho]stellt eine nichtlineare funktionale Kopplung des Systemzustands an das Signalfeld dar.
Dieser Begriff kann phänomenologisch wie folgt modelliert werden:
\mathcal{L}_{\chi}[\rho] = f(\chi),(\rho^2 - \rho,\mathrm{Tr}[\rho^2]),
Einführung einer zustandsabhängigen Verstärkung oder Dämpfung, die für reine Zustände verschwindet (\rho^2 = \rho).
4. Informationskapazität
Das wichtigste Ergebnis ist, dass die postselektierte oder nichtlineare Detektion eine kleine, aber endliche klassische Kapazität ergeben kann C_{\mathrm{eff}} über einen Kanal, der sonst nur Verschränkung (keine Signalisierung) ermöglichen würde:
C_{\mathrm{eff}} \approx p_{W}, C,
woher p_{W} ist die Erfolgswahrscheinlichkeit des nichtlinearen Post-Selection-Fensters und C ist die Kapazität eines idealisierten Signalkanals.
Dies entspricht einer winzigen, aber messbaren Abweichung vom strikten Nicht-Kommunikationsverhalten in aktivierten Medien:
C_{\mathrm{eff}} > 0, \qquad C_{\mathrm{eff}} \ll C_{\mathrm{klassisch}}.5. Physikalisches Beispiel: QCT-Barrierekopplung
In einem quantengekoppelten Transistor fungieren die beiden Graphenschichten als lokal kohärente Detektoren, die über eine Quantenbarriere verbunden sind.
Das effektive Signalfeld \Zettel) stellt das evaneszente Phasenpotential über der h-BN-Tunnelregion dar.
Die Nichtlinearität tritt durch die spannungsabhängige Barrieretransparenz ein:
T_{\chi}(V) = T_{0} \exp[-\alpha (1 - \beta V + \epsilon, \Phi_{\chi}(\rho))],
woher \Phi_{\chi}(\rho) ist ein schwacher Rückkopplungsterm, der die lokale Wellenfunktionskohärenz mit dem Feldzustand koppelt.
Eine solche Rückkopplung verändert die Tunnelwahrscheinlichkeit nichtlokal, erhält aber die globale Unitarität.
6. Erhaltung und Stabilität
Um eine außer Kontrolle geratene Verstärkung zu verhindern, erfüllt der nichtlineare Term eine Erhaltungsbedingung:
\mathrm{Tr}[\rho,\mathcal{L}_{\chi}[\rho]] = 0,
Sicherstellen, dass die Gesamtwahrscheinlichkeit und Energie in erster Ordnung konstant bleiben \Epsilon.
Dadurch bleibt die Dynamik selbstkonsistent und begrenzt – überlichtschnelle Paradoxe werden vermieden, während gleichzeitig eine unterbeobachtbare, kohärente Signalübertragung möglich ist.
7. Deutung
Das Ergebnis ist ein minimal modifizierte Quantenregel:
die Detektorreaktion ist leicht nichtlinear und zustandsabhängig, was zu einer kleinen Abweichung vom strengen Nicht-Kommunikationstheorem führt, während die Born-Regel-Normalisierung global beibehalten wird.
In aktivierten Bereichen (z. B. h-BN-Barrierefeldern, nachselektierten Koinzidenzschaltungen) verhält sich die Interaktion so, als ob Phaseninformationen durch die Quantenlücke tunneln könnten – und dabei ein winziges, endliches klassisches Signal über raumartige Trennung hinweg transportieren könnten, ohne die Unitarität oder globale Kausalität zu verletzen.
Gemeinsam kein Frontalunterricht. Quantenmechanik überall neu schreiben. Wir fügen hinzu winzige, zustandsabhängige Wendung wie der Detektor/Verstärker innerhalb der Lücke reagiert – gerade genug, um ein schwaches Muster auf dem Rauschen zu erzeugen. Außerhalb der Lücke ist alles normal und linear. Innerhalb der Lücke ist die Reaktion leicht kontextbewusst (das ist der „nichtlineare“ Teil), und wir behalten es begrenzt damit nichts wegläuft.
Analogie: Ein Mikrofon mit einem subtilen eingebauten Kompressor, der nur in einem winzigen Sweet Spot aktiv ist – die meiste Zeit ist er transparent, aber an dieser Stelle formt er das Signal gerade genug, um gehört zu werden.
4. Experimentelle Vorhersagen
- Milde Rahmenanisotropie: Die Signalgeschwindigkeit hängt von der Ausrichtung mit ab uᵃ
- Evaneszente → propagierende Konvertierung unter QCT-Bias-Modulation
- Gesteuert Verletzung der Tsirelson-Grenze
- Verzögerungsskalierung mit Junction-Bias, nicht mit Barrieredicke
5. Testprotokolle
- Zwei-Labor-QCT-Test: Die Vorspannungsmodulation am Knoten A erzeugt eine korrelierte Reaktion am Knoten B außerhalb des Lichtkegels.
- Moving-Frame-Swap: In relativer Bewegung wiederholt, um die bevorzugte Rahmenausrichtung zu testen.
- Evaneszente Injektion: Unterhalb des Cutoff-Bereichs liegender Wellenleiter, der in die QCT-Lücke gekoppelt ist, um eine phasenmodulierte Wiederherstellung zu erkennen.
6. Rolle des QCT
Das Femtosekunden-Tunnel- und NDR-Verhalten des QCT erzeugt eine begrenzte Nichtlinearität, die notwendig ist für steuerbare überlichtschnelle Kohärenz. Die Kausalität wird durch die No-Loop-Beschränkung aufrechterhalten, wodurch eine globale Ordnung gewährleistet wird.

Zusammengefasst: CFS bewahrt die Relativität fast überall und ermöglicht gleichzeitig einen strukturierten Signalkegel, der nur in bestimmten Quantenmedien wie der QCT aktiv ist. Dieses Framework führt ein überprüfbare Vorhersagen für überlichtschnelle und dennoch kausal konsistente Kommunikation.
Dieser Artikel ist Teil einer Serie, die sich ausschließlich auf eine unerklärliche Sichtung bezieht, die ich 1986 in Irland hatte:
- Vorahnung der Challenger-Katastrophe
- UFO über der Galway Bay, Kapitel 1: Die Salthill-Begegnung von 1986
- Der Black UFO Report: Prinz Charles, ein Jumbo-Jet und eine Nacht voller Luftgeheimnisse
- UFO über der Galway Bay, Kapitel 2: Psychischer Mayday von einem abgestürzten UFO
- UFO über der Galway Bay, Kapitel 3: Die irischen Tuatha Dé Danann als kosmische Besucher
- Ansehen und hören Sie: „Die Ankunft der Tuatha Dé Danann“ Music Video
- UFO über der Galway Bay, Kapitel 4: Reverse Engineering des quantengekoppelten Transistors
- Der quantengekoppelte Transistor (QCT): Die Leere verstärken
- Können Informationen schneller als das Licht reisen? - Ohne die Physik zu brechen?