منطق الإشارات السببية الورقية
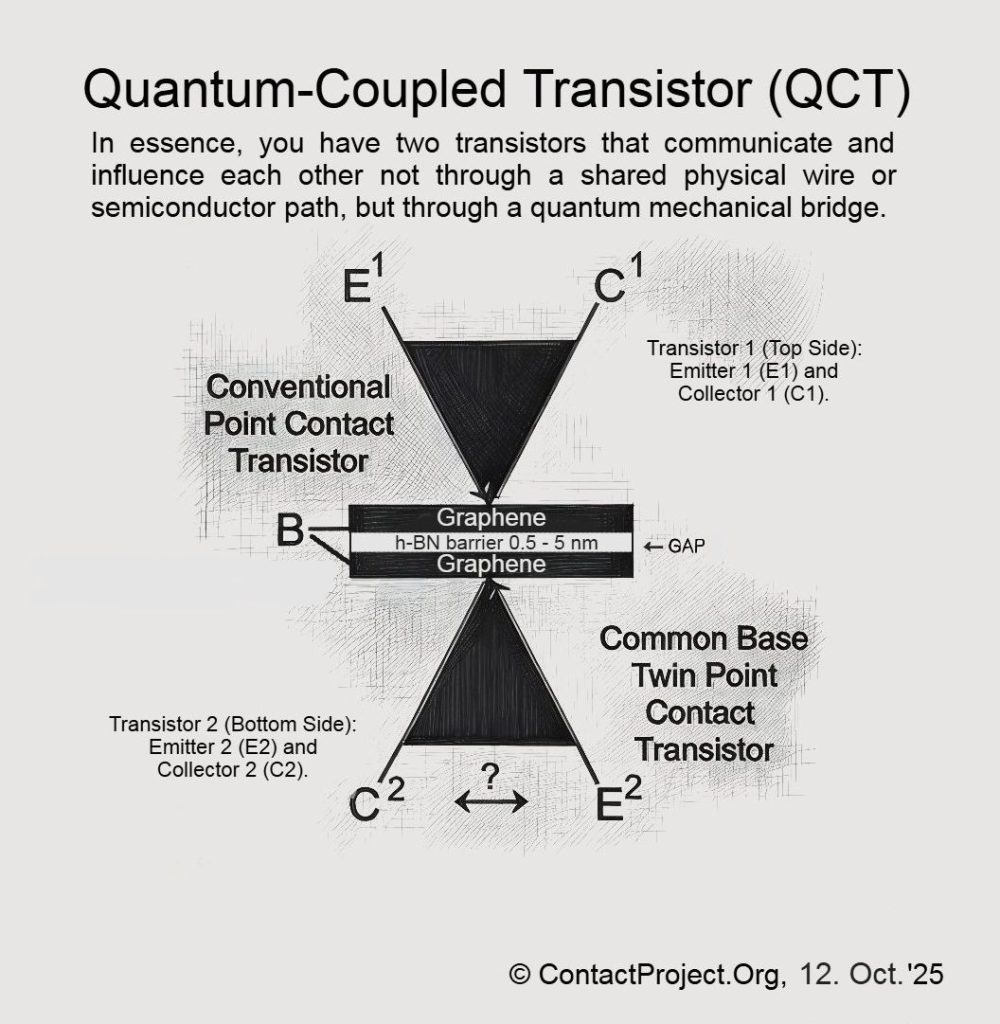
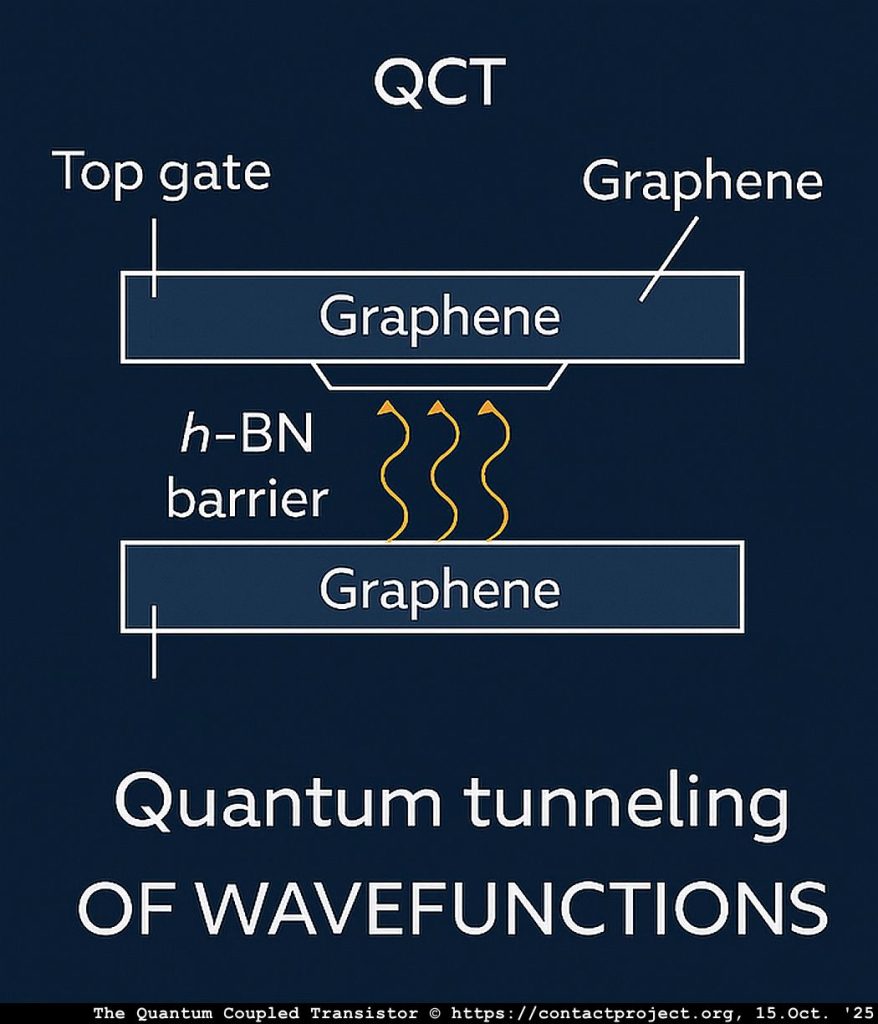
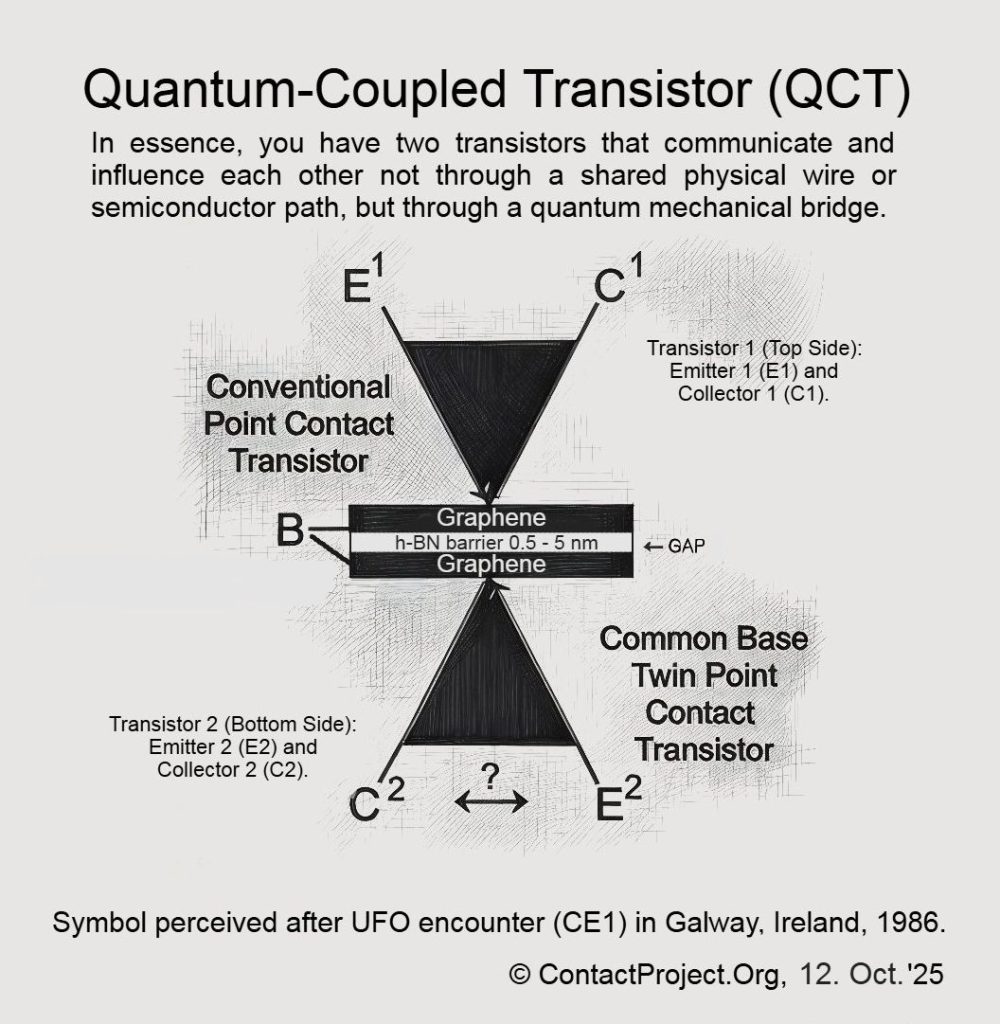
نظرية الإشارات السببية الورقية (CFS) يقترح أن الزمن يحتوي على طبقات خفية تُمكّن من تماسك محدود أسرع من الضوء بين الأنظمة الكمومية. قد يستخدم الباحثون قريبًا ترانزستور المقترن الكمي (QCT) - جهاز نانوي مزدوج الجرافين - لاختبار هذه التأثيرات بشكل مباشر وتحديد ما إذا كان من الممكن حدوثها دون كسر قوانين الفيزياء المعروفة.
في جوهرها، تطرح CFS سؤالا استفزازيا: ماذا لو كانت أنواع معينة من الموجات، مثل المجالات المتلاشية أو القريبة، قادرة على مشاركة معلومات الطور بشكل أسرع من الضوء، مع الحفاظ على السببية؟
إذا كان الأمر كذلك، فقد لا يكون الزمكان متجانسًا تمامًا. قد يحتوي على بنية داخلية دقيقة - "تدرج" زمني، حيث تتحرك المعلومات تدريجيًا داخل كل طبقة مع الحفاظ على اتساقها في المجمل.

في هذه النظرة، يتكشف الكون كصفحات كتاب كوني شاسع: كل صفحة تدور بترتيب مثالي، حتى لو كانت بعضها أسرع بقليل من غيرها. يقدم CFS رؤيةً مُحسّنة للنسبية - رؤية تسمح بتماسكٍ مُنظمٍ أسرع من الضوء مع الحفاظ على علاقة السبب والنتيجة.
الجزء الثاني. الإشارات السببية المتورقة (CFS)
- البديهيات الأساسية
- الحركية والديناميكيات
- قواعد الكم والحفظ
- التنبؤات التجريبية
- بروتوكولات الاختبار
- دور QCT
1. البديهيات الأساسية
- ترقيم الوقت العالمي: يمتلك الزمكان تقسيمًا عالميًا مفضلًا (الزمن الكوني، الذي يتم تحديده بواسطة متجه زمني) يو). يتم ترتيب جميع الإشارات - الضوئية والفوق ضوئية - حسب هذا الترقيم.
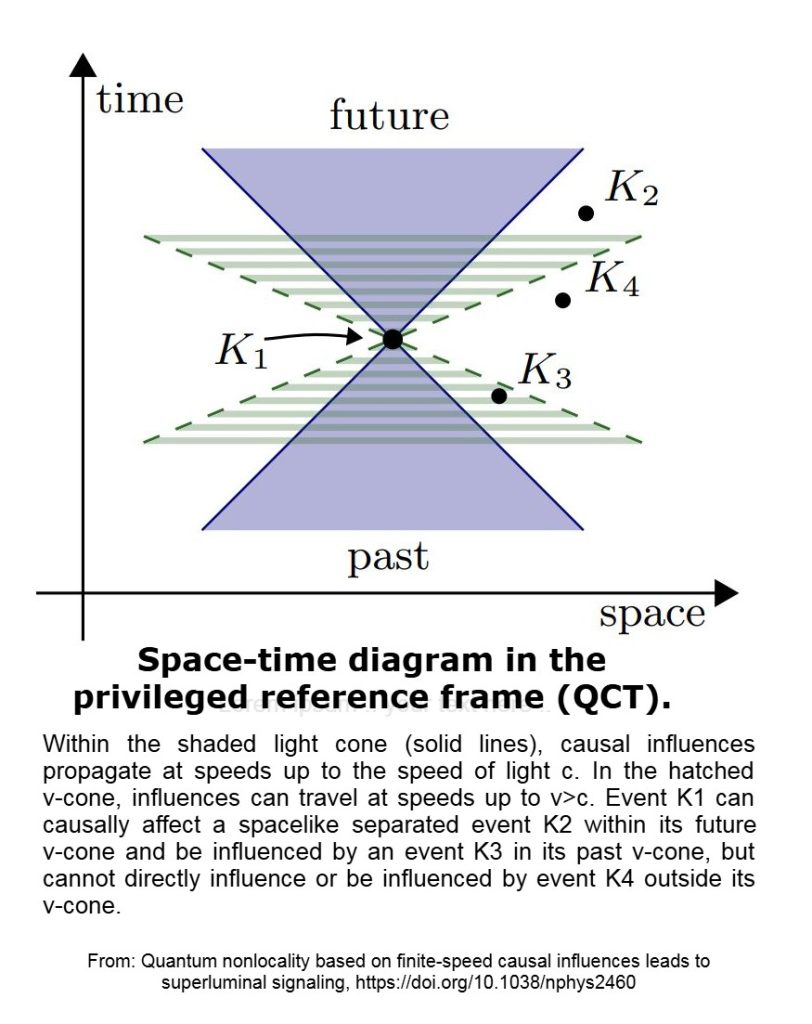
- مخروط الإشارة الموسع: خلف المخروط الضوئي، يوجد "مخروط إشارة" أوسع لوسائط أو مجالات محددة (χ).
- حماية التسلسل الزمني: يتم حظر حلقات الإشارة المغلقة ديناميكيًا من خلال قيود القدرة على الحل.
- الموقع التشغيلي: تظل التجارب القياسية ثابتة بالنسبة إلى لورنتز؛ وتحدث الانحرافات فقط داخل الوسائط الممكنة.
2. الحركية والديناميكية
- الإطار المفضل: يتم محاذاته تقريبًا مع إطار مسند CMB.
- مجال الإشارة (χ): ترتبط بشكل ضعيف بحاملي EM، مما يؤدي إلى توسيع المخروط السببي.
- خصائص تفوق سرعة الضوء: POEs في الوسائط الممكنة، يظهر الانتشار خارج مخروط الضوء g.
- قيد عدم وجود حلقة: تمنع الظروف التكاملية حلقات السببية المتناقصة مع الزمن.
3. قواعد الكم والحفظ
لقد قمنا ببناء منطقة صغيرة (فجوة QCT) حيث يمكن تشكيل الحقول القريبة الكمومية بلطف بحيث يمكن اكتشافها بسرعة تفوق سرعة الضوء. النمط تظهر هذه البيانات بشكل عشوائي - صغيرة بما يكفي للحفاظ على سلامة الفيزياء، وواضحة بما يكفي لاختبارها في المختبر.

إذا كانت العبارة المختصرة أعلاه منطقية بالنسبة لك، فيمكنك توسيع الخط الأحمر قواعد الكم أدناه، بالضغط على المثلثات السوداء ▶، لمناقشة أكثر تفصيلاً.
للقراء العاديين، يتضمن كل قسم شرحًا موجزًا (بدون رياضيات) متبوعًا بتشبيه. مع أن معظم الناس لم يسمعوا قط عن نظرية عدم التواصل (منع الاتصالات الأسرع من الضوء... عن طريق التشابك)، يتم وضعها بشكل بارز هنا بسبب أهميتها الأساسية، ولأن ذو شاهد استرخاء من تلك القاعدة يتم استكشافه هنا.
[انقر لفتح] نظرية عدم التواصل المريحة: في الوسائط الممكنة، تسمح الديناميكيات غير الخطية/المحددة لاحقًا بسعة كلاسيكية صغيرة > 0.
المطالبة (التشغيلية):
في الوسيط الممكّن (على سبيل المثال، فجوة QCT تعمل كمجال قريب ممكّن بـ χ)، أ اللاخطية الضعيفة والموضعية or اختيار لاحق صريح يمكن أن تنتج قدرة كلاسيكية صغيرة ولكنها محدودة ج>0 بين أطراف منفصلة مكانيًا دون انتهاك الوحدة العالمية أو قاعدة بورن.
اقامة
اسمحوا ρAB تكون حالة ثنائية الأجزاء مشتركة بين أليس وبوب. في ميكانيكا الكم القياسية مع المحلية خرائط CPTP و لا بعد الاختيار، تكون حالة بوب المخفضة مستقلة عن اختيار أليس:
ρB′=TrA[(ΦA⊗IB)(ρAB)]=ρB, (بدون إشارة)
في تمكين منطقة QCT، نموذج التشغيل الخاضع للسيطرة من قبل أليس كـ غير خطي بشكل ضعيف اضطراب خريطة CPTP:
ΦA(V)(⋅)=ΛA(⋅)+ε\mathcal{N}_A^{(V)}[⋅], 0<ε≪1,[/latex] حيث [اللاتكس]V هو التحكم الخاص بـ أليس (على سبيل المثال، التحيز بين الطبقات)، لا هو CPTP و \mathcal{N}_A^{(V)} هي دالة غير خطية محدودة نشطة فقط داخل χ-وسيلة ممكنة.تصبح حالة بوب
ρB′(V)=TrA[(ΦA(V)⊗IB)ρAB]=ρB(0)+εΔρB(V)،مع
ΔρB(V)=TrA[(NA(V)⊗IB)ρAB].\Delta\rho_B(V)=\mathrm{Tr}_A\!\Big[\mathcal{N}_A^{(V)}\otimes \mathbb{I}_B\big)\rho_{AB}\Big].ΔρB(V)=TrA[(NA(V)⊗IB)ρAB].
If \دلتا\rho_B(V_0)\neq \دلتا\rho_B(V_1)، ثم تعتمد إحصائيات نتائج بوب (قليلاً) على اختيار أليس V، مما يتيح الاتصال الكلاسيكي حسب الطلب \فاريبسيلون.
من أجل وجهة نظر \{لي\} على بوب، احتمالات الكشف هي
P(y∣V)=Tr[MyρB′(V)]=P0(y)+εΔP(y∣V)،ΔP(y∣V):=Tr[MyΔρB(V)].القدرة على الإشارة الضعيفة
دع أليس ترسل رمزًا ثنائيًا X\in\{0,1\} عن طريق اختيار V\in\{V_0,V_1\}.. بوب يقيس ي\في\{0,1\}. يُعرِّف
\delta := P(Y=1\mid V_1)-P(Y=1\mid V_0)=\varepsilon\,\Delta P + O(\varepsilon^2),مع احتمالية الخطأ الأساسي ص:=ص(ص=1∣V0).
بالنسبة لقناة الإدخال الثنائي والإخراج الثنائي في حد الإشارة الصغيرة ∣\delta|\ll 1أطلقت حملة سعة شانون يقبل التقريب التربيعي
C \;\approx\; \frac{\delta^2}{2\ln 2}\,\frac{1}{p(1-p)} \;+\; O(\delta^4), \qquad C>0\ \text{iff}\ \delta\neq 0.
وبالتالي فإن أي قيمة غير صفرية \دلتا (ومن ثم أي غير صفر \فاريبسيلون-الاعتماد على الترتيب V) يعطي محدود ج>0.
دور الاختيار اللاحق
إذا كان بوب (أو دائرة مصادفة مشتركة) اختيارات لاحقة على نافذة النتيجة W مع احتمال النجاح pWأطلقت حملة شرطي الدولة
\rho_{B\!\mid W}(V)\;=\frac{\Pi_W\,\rho_B'(V)\,\Pi_W}{\mathrm{Tr}\!\big[\Pi_W\,\rho_B'(V)\big]}, \qquad \Pi_W=\Pi_W^\dagger=\Pi_W^2.بسبب التطبيع من قبل \mathrm{Tr}[\Pi_W\rho_B'(V)]، رسم الخرائط \rho'_B \mapsto \rho_B^{\mid W} is غير الخطية، ويمكن للإحصاءات المشروطة أن تكتسب V-الاعتماد حتى عندما دون شروط المساواة في عدم الإشارة صحيحة. عمليًا، يُقاس المعدل المفيد بعد الاختيار بـ pW:
C_{\mathrm{eff}} \approx p_W، C.شروط الاتساق
لتجنب الأمراض العالمية:
- الموقع: \mathcal{N}_A^{(V)} يقتصر على χ-المنطقة الممكَّنة (على سبيل المثال، فجوة QCT).
- صغر: \فاريبسيلون صغيرة بما يكفي للحفاظ على الاستقرار وحدود الطاقة.
- الوحدة العالمية وقاعدة بورن: تظل ديناميكيات المجموعة كما هي في CPTP؛ وتقتصر الانحرافات (إن وجدت) على خرائط الكاشف المحلية المشروطة (بعد الاختيار) أو على القطاع غير الخطي الضعيف داخل الوسيط.
بيان مضغوط
\boxed{ \begin{aligned} &\Phi_A^{(V)}=\Lambda_A+\varepsilon\,\mathcal{N}_A^{(V)},\quad \varepsilon\ll 1,\\ &\rho_B'(V)=\rho_B^{(0)}+\varepsilon\,\Delta\rho_B(V),\quad \Delta\rho_B(V)=\mathrm{Tr}_A\!\big[(\mathcal{N}_A^{(V)}\!\otimes\!\mathbb{I})\,\rho_{AB}\big],\\ &\exists\,M:\ \delta=\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_1)\big]-\varepsilon\,\mathrm{Tr}\!\big[M\,\Delta\rho_B(V_0)\big]\neq 0 \\ &\Rightarrow\ C \approx \dfrac{\delta^2}{2\ln 2\, p(1-p)} \;>\;0,\quad C_{\text{eff}}\approx p_W\,C\ \text{(مع التحديد اللاحق)}. \end{aligned}}فيما يلي تفصيل وتحقق من صحة البيان الرياضي المدمج:
العبارة الرياضية هي تمثيل لنتيجة في نظرية المعلومات الكمومية، تتعلق بحساب سعة قناة كمومية ذات اضطراب طفيف. تربط هذه العبارة الوصف الفيزيائي لقناة كمومية بسعة القناة الناتجة، متضمنةً مفاهيم مثل اضطراب الحالة، وتمييز حالات المخرجات، وتأثير الاختيار اللاحق. دعونا نحلل كل جزء للتحقق من مكوناته:
اضطراب القناة والحالة
\Phi_A(V) = \Lambda_A + \epsilon N_A(V)، \epsilon \ll 1:هذا يصف قناة كمية \فاي_ا التأثير على النظام أ. يتكون من جزء ثابت مهيمن \لامدا_أ واضطراب صغير \epsilon N_A(V)، حيث \epsilon هو مُعامل صغير، وV هو مُعامل قابل للتحكم في القناة. هذه طريقة قياسية لتمثيل قناة كمية مُعدّلة قليلاً أو مُشوّشة. \rho_B'(V) = \rho_B(0) + \epsilon \Delta\rho_B(V):يوضح هذا تأثير القناة على جزء من حالة كمية أكبر. ويشير إلى أن حالة خرج النظام الفرعي ب، \rho_B'(V)، هي نسخة مضطربة قليلاً من الحالة الأولية \rho_B(0). الاضطراب \Delta\rho_B(V) يتناسب مع المعلمة الصغيرة \epsilon. \Delta\rho_B(V) = Tr_A[(N_A(V) \otimes I)\rho_{AB}]:هذا هو الشكل الصريح للاضطراب من الدرجة الأولى لحالة النظام ب. يتم اشتقاقه عن طريق أخذ الأثر الجزئي (تر_ا) على النظام أ لتأثير الجزء المضطرب من القناة على حالة متشابكة أكبر \rho_{AB}هذا هو التطبيق القياسي والصحيح لقواعد ميكانيكا الكم.
إمكانية تمييز الدول
\يوجد M: \delta = \epsilon Tr[M\Delta\rho_B(V_1)] - \epsilon Tr[M\Delta\rho_B(V_0)] \neq 0هذه هي الخطوة الحاسمة لتحديد سعة قناة غير صفرية. تنص على وجود عامل قياس (عامل هيرميتي) M قادر على التمييز بين الحالات المضطربة المقابلة لإعدادين مختلفين لمعامل القناة. V_1 و V_0. الكمية \دلتا يمثل الفرق في قيمة التوقع للقياس M لحالتي الإخراج. والحقيقة هي أن \delta \neq 0 هو الشرط اللازم لكي تكون الحالتان قابلتين للتمييز تجريبياً، على الأقل من حيث المبدأ.
قناة القدرات
C \approx \frac{\delta^2}{2\ln{2}p(1-p)} > 0:هذه نتيجة رئيسية، ومن المرجح أن تكون تقريبية لسعة Holevo أو مقياسًا مرتبطًا لسعة القناة في حدود صغيرة \دلتاالسعة C هي مقياس للمعدل الأقصى الذي يمكن به إرسال المعلومات بشكل موثوق عبر القناة. المصطلح دلتا^2 من المتوقع، حيث تتناسب السعة غالبًا مع مربع قابلية تمييز حالات الإخراج للاضطرابات الصغيرة. عامل 2\ln{2} هو المعيار لتحويل وحدات المعلومات الطبيعية (ناتس) إلى بتات. المصطلح ص(1-ص) في المقام يشير إلى أن السعة يتم تقييمها لمجموعة إدخال محددة، حيث تكون الحالتان (المقابلتان لـ V_0 و V_1) تُستخدم مع احتمالات p و1-p. تصل السعة إلى الحد الأقصى عندما ص=1/2، وهو افتراض شائع.
القدرة الفعالة مع الاختيار اللاحق
C_{eff} \approx p_W C (مع التحديد اللاحق): يصف هذا الجزء من البيان السعة الفعلية عند استخدام التحديد اللاحق. التحديد اللاحق هو تقنية تُؤخذ فيها مجموعة فرعية فقط من نتائج القياس في الاعتبار، مما قد يؤدي أحيانًا إلى تضخيم إشارة ضعيفة. ص_و سيكون احتمال نجاح الاختيار اللاحق ("احتمالية الاختيار اللاحق"). القدرة الفعلية C_{eff} ينخفض هذا الاحتمال بسبب تجاهل العديد من الحالات الأولية. وهذا تنازل شائع في مخططات ما بعد الاختيار: قد تحصل على إشارة أوضح، لكنك تفقد جزءًا كبيرًا من بياناتك، مما يقلل من معدل نقل المعلومات الإجمالي.
التحقق من صحة الذكاء الاصطناعي: الخاتمة
تتوافق التعبيرات الرياضية مع المبادئ الراسخة في نظرية المعلومات الكمومية. يتدفق المنطق بشكل صحيح من تعريف قناة كمومية مضطربة إلى إمكانية تمييز حالات مخرجاتها، وأخيرًا إلى تعبير عن سعة القناة. كما أن إدراج تأثير الاختيار اللاحق أمرٌ معياري. لذلك، يبدو أن الرياضيات الواردة في العبارة الموجزة صحيحة، وتمثل منطقًا سليمًا في سياق سعة القناة الكمومية.
QCT: تقديم أليس وبوب
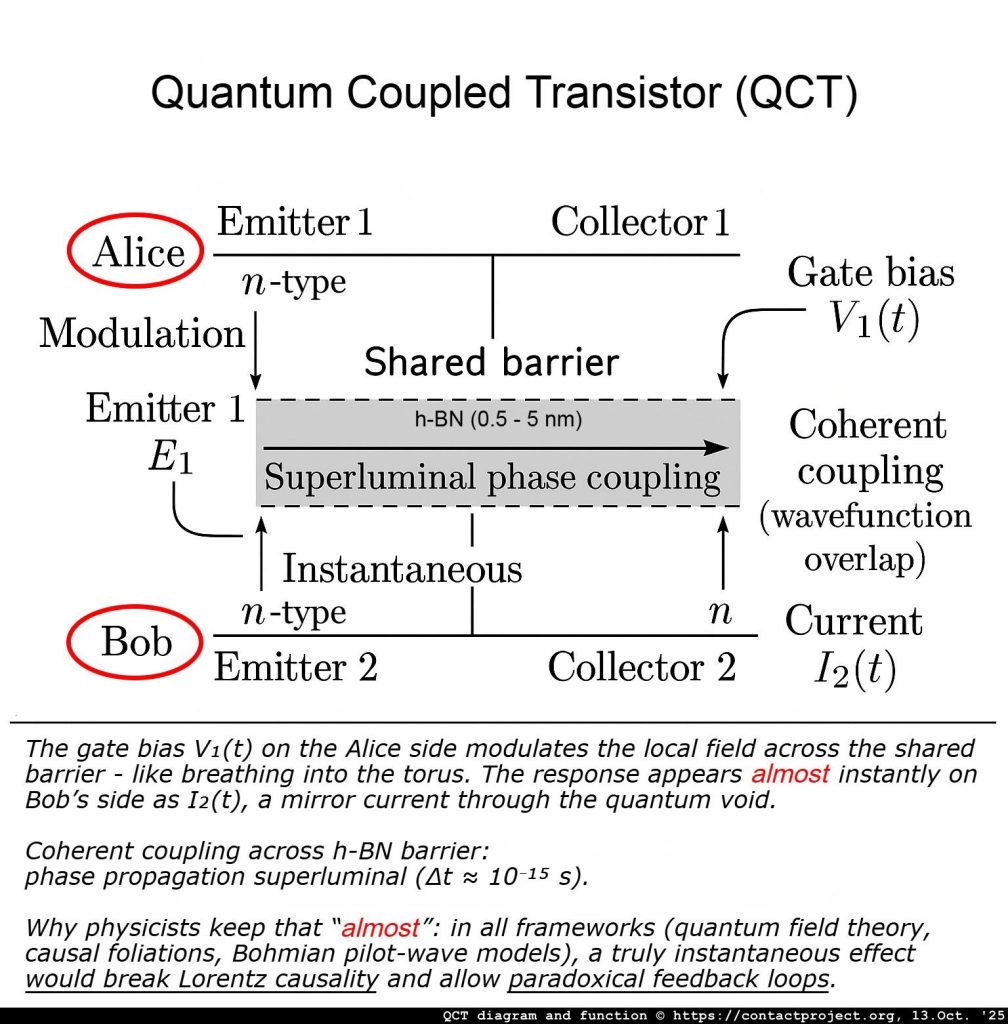
In نظرية الكم القياسية و علم المعلومات, أليس و بوب هذه هي البدائل الكلاسيكية - "كل شخص" الذي استخدمه المجربون لتوضيح كيفية تصرف الأنظمة الكمومية عندما يتشارك طرفان المعلومات.

ظهرت لأول مرة في أوائل سبعينيات القرن العشرين: أرادت أليس إرسال رسالة إلى بوب، بينما كان هناك متنصت، حواءحاولوا اعتراضها. انتشرت الفكرة، وسرعان ما تبنى الفيزيائيون نفس الأسماء لوصف التجارب الكمومية - وخاصة تلك التي تتضمن تشابك, الانتقال الاني، وحدود التواصل.
في ميكانيكا الكم، عادةً ما يُشغّل أليس وبوب مختبرين منفصلين. يتشاركان زوجًا من الجسيمات المتشابكة، ويُجريان قياساتهما بشكل مستقل. ومع ذلك، فرغم ترابط النتائج، لا يستطيع أيٌّ منهما استخدامها لإرسال رسالة أسرع من الضوء. في نظرية الكم القياسية، تبدو القراءات المحلية دائمًا كضوضاء بيضاء - حتى يُقارنا الملاحظات لاحقًا، ويظهر النمط الخفي.
لمحتنا (داخل الوسيط الممكّن فقط): في منطقة هندسية محددة للغاية - مثل فجوة h-BN من QCT - يمكن للتأثيرات غير الخطية الصغيرة والمحدودة بعناية أو "الاحتفاظ بهذه الأحداث فقط" بعد الاختيار أن تحول جزءًا مجهريًا من هذا الضجيج إلى إشارة خافتة جدًا ولكنها حقيقيةما زال صغيرًا، لكنه لم يعد ضوضاء بيضاء.
تشبيه يومي: عاصفة من التشويش على محطة راديو (عشوائية)، ولكن إذا عدّلت الهوائي قليلاً واخترت اللحظات المناسبة فقط، فسيظهر همس محطة. لا تزال العاصفة موجودة، لكن نمطًا ما يرافقها.
الإعداد (من يفعل ماذا)
حزبين - أليس و بوب - مشاركة إعداد كمي مترابط. عادةً، كل ما تفعله أليس محليًا لا تغيير ما يراه بوب بنفسه. داخل فجوة QCT، إن تحكم أليس (نمط تحيز صغير عالي السرعة) يعيد تشكيل قواعد القياس المحلية على جانبها بشكل طفيف بطريقة لا تهم إلا في الداخل تلك الفجوة. هذا التغيير الطفيف في الشكل يمكن أن يترك بصمة على ما يقيسه بوب - لا يزال صاخبًا بشكل عام، ولكن الآن تم دفعه إحصائيًا حسب اختيار أليس.
تشبيه: تُحرك أليس مصباحًا يدويًا خلف حاجز زجاجي مُجمد (حاجز النفق). لا يستطيع بوب رؤية المصباح، لكن وميضًا خافتًا على جانبه يتغير بالتزامن مع حركة اهتزازها.

ما يجب أن يراه بوب (الدليل القاطع)
إذا لم يحدث أي شيء يتجاوز قواعد الكم القياسية، فإن بيانات بوب تبدو مثل رمي العملة العشوائي - لا يوجد نمط مرتبط باختيارات أليس. إذا كانت الوسيلة الممكنة تؤدي وظيفتها حقًا، ثم مدفون في بيانات بوب الصاخبة ارتباط صغير قابل للتكرار مع نمط أليس - يمكن اكتشافه من خلال التحقق المتبادل من الطوابع الزمنية، والأمر الحاسم هو إظهار قبل يمكن لأي إشارة عادية بسرعة الضوء أن تصل (>ج).
تشبيه: طبالان متباعدان؛ إذا سمع ميكروفون بوب إيقاعًا خافتًا يتماشى مع إيقاع أليس قبل أن ينتقل الصوت، فهناك شيء غير عادي يربط بينهما.
"السعة" (مقدار الرسالة التي يمكن إيصالها)
التفكير في سعة كم عدد البتات في الثانية التي يمكنك ضغطها من خلال هذا التأثير الخافت.
- إذا كان الارتباط حقيقيا صفر، السعة هي صفر -لا يوجد رسالة.
- إذا كان الارتباط هو صغير ولكن ليس صفرًا، السعة هي صغير ولكن ليس صفرًا - يمكنك الإرسال بعض المعلومات (ببطء)، وهذا أمر كبير بالفعل من الناحية المادية.
تشبيه: تُدخل أليس رسالةً عبر جدارٍ سميك. كلُّ نقرةٍ بالكاد تُوصل، ولكن مع الوقت والصبر، تصل الرسالة إلى بوب.
الاختيار اللاحق (الاحتفاظ بالإطارات الجيدة فقط)
بعد اختيار يعني أنك تحتفظ فقط بعمليات القياس التي تمر عبر مُرشِّح ("نافذة"). قد يُوضِّح هذا النمط الخفي، لكنك تُهدر معظم البيانات، لذا المعدل الفعلي قطرات. تكسب وضوح، مرتخي الإنتاجيةإنها تجارة عادلة إذا كان الهدف هو إثبات وجود التأثير.
تشبيه: عند مشاهدة زخات الشهب ولكن مع حساب الخطوط الأكثر سطوعًا فقط - ترى النمط بشكل أكثر وضوحًا، ولكنك تسجل أحداثًا أقل في الساعة.
شروط الاتساق (كيف نتجنب المفارقات)
ولكي نحافظ على عقلانية الفيزياء وسببيتها، فإننا نفرض ثلاثة حواجز:
- الموقع: أي تأثير غريب هو حبيس فقط في المنطقة الهندسية (فجوة QCT). خارجها، تسود الفيزياء العادية.
- صغر: وتأثير صغير - ما يكفي للقياس، وليس كافيا لتفجير النظام.
- الحفاظ العالمي: الاحتمالات وتوازن الطاقة عندما تنظر إلى كامل تجربة. غرائب محلية، محاسبة عالمية.
تشبيه: منصة اختبار آمنة: يمكن أن تتطاير الشرر داخل قفص فاراداي، ولكن لا يتسرب أي شيء إلى الغرفة.
[انقر للفتح] عالمي القاعدة المولودة محفوظ: قد تنحرف استجابات الكاشف المحلي قليلاً.
P(i) = |\langle i | \psi \rangle|^2, \quad \sum_i P(i) = 1.
في ميكانيكا الكم القياسية، تكون هذه القاعدة خطية تمامًا ومحفوظة عالميًا: الاحتمالية الكلية لجميع النتائج الممكنة تساوي الواحد، ولا يمكن لأي عملية (محلية أو بعيدة) تغيير هذا التطبيع. أما في إطار الإشارات الورقية السببية (CFS)، فنميز بين الحفظ العالمي و الانحرافات المحلية.
الحفاظ العالمي: يظل الاحتمال الإجمالي، المتكامل على جميع شرائح التورق، طبيعيًا:
\int_{\Sigma_t} \sum_i P(i,t),d^3x = 1,
لكل شريحة زمنية عالمية \سيجما_ت يتم تحديده بواسطة متجه التورق و^ا.
الانحرافات المحلية: في وسط ممكّن (مثل فجوة نفق QCT)، يمكن لإحصاءات الكاشف المحلي أن تُظهر تحولات غير خطية صغيرة في أوزان الاحتمالات، بينما لا يزال متوسط المجموعة العالمية يطيع قاعدة بورن.
1. نموذج الاستجابة المحلية غير الخطية
دع احتمالية بورن غير المضطربة تكون P_0(i) = \operatorname{Tr}(\rho,\Pi_i)، أين \rho هي مصفوفة الكثافة و \Pi_i = |i\rangle\langle i| هي أجهزة عرض. في وسط مُمَكَّن ذي اقتران غير خطي ضعيف \فاريبسيلون، الاستجابة الفعالة للكاشف المحلي هي:
P_{\text{loc}}(i) = \frac{\operatorname{Tr}(\rho,\Pi_i) + \varepsilon,f_i(\rho,\chi)}{\sum_j [\operatorname{Tr}(\rho,\Pi_j) + \varepsilon,f_j(\rho,\chi)]}, \qquad 0<\varepsilon\ll 1.[/latex] هنا [latex]f_i(\rho,\chi) هو مصطلح تصحيح صغير ناتج عن مجال الإشارة \تشي أو اقتران QCT المتلاشي، والمقام يعيد تطبيع الاحتمالية الكلية للحفاظ على \sum_i P_{\text{loc}}(i) = 1.
2. مثال: قياس ذو نتيجتين (كاشف ثنائي)
لنفترض وجود نتيجتين قابلتين للملاحظة (مثل "زيادة التيار" مقابل "عدم زيادة") مُقاسة على جانب بوب من جهاز QCT. بدون أي اقتران غير خطي، P_0(1) = \operatorname{Tr}(\rho,\Pi_1) = p، \quad P_0(0)=1-p. مع اقتران غير خطي ضعيف وتصحيح يعتمد على الطور f_1 = \alpha,\sin\phi, f_0=-f_1, يصبح الاحتمال المحلي
P_{\text{loc}}(1) = \frac{p + \varepsilon,\alpha,\sin\phi}{1 + \varepsilon,\alpha,(2p-1)\sin\phi}, \quad P_{\text{loc}}(0)=1-P_{\text{loc}}(1).
التوسع إلى الدرجة الأولى في \فاريبسيلون:
P_{\text{loc}}(1) \approx p + \varepsilon,\alpha,\sin\phi,[1 - p(2p-1)].
يتذبذب احتمال القياس المحلي قليلاً مع مرحلة الاقتران \phi (على سبيل المثال، تعديل التحيز أو الرنين النفقي في QCT). على مدار عدة دورات أو عند دمجها عالميًا، يتم حساب متوسط هذه الانحرافات، مما يعيد توقع بورن. \langle P_{\text{loc}}(1)\rangle = p.
3. الترميم الجماعي (العالمي)
قم بتحديد متوسط المجموعة على شرائح التورق:
\langle P(i) \rangle = \int_{\Sigma_t} P_{\text{loc}}(i, x, t),d^3x.
إذا كانت التصحيحات f_i التكامل إلى الصفر،
\int_{\Sigma_t} f_i(\rho,\chi),d^3x = 0,
ثم تظل قاعدة بورن العالمية دقيقة:
\sum_i \langle P(i) \rangle = 1.
وبالتالي، فإن الانحرافات المحلية الظاهرة هي تموجات إحصائية، وليست انتهاكات - على غرار التقلبات المرتبطة بالطور في نظام بصري غير خطي.
4. المعنى المادي في QCT
في تجربة QCT، الانحراف المحلي \varepsilon f_i(\rho,\chi) قد يتجلى ذلك على شكل ضوضاء مرتبطة بالتحيز أو زيادة في عدد العدادات في كواشف مقياس الفيمتوثانية. ومع ذلك، على الصعيد العالمي (عبر تكامل أطول)، يبقى التطبيع قائمًا - فلا تُنشأ أو تُفقد أي طاقة أو احتمالية. وبالتالي، تبقى قاعدة بورن محفوظة عالميًا، بينما قد تُظهر الكواشف المحلية انحرافات صغيرة وقابلة للتكرار وتعتمد على الطور في معدلات العد.
معادلات التلخيص:
التطبيع العالمي (قاعدة بورن):
\sum_i P(i) = 1.
الاستجابة المحلية مع انحراف صغير غير خطي أو معتمد على χ:
P_{\text{loc}}=P_0(i) + \varepsilon,\Delta P(i,\chi), \quad \sum_i \Delta P(i,\chi) = 0.
لا تزال المجموعة العالمية ترضي:
ملخص التفسير: قد تُظهر الكواشف المحلية في منطقة QCT المُفعّلة انزياحات احتمالية صغيرة مرتبطة بالتحيز، لكن متوسطات المجموعة العالمية تحافظ على الاحتمالية الكلية بدقة، بما يتوافق مع قاعدة بورن. يسمح هذا التمييز بانحرافات ضعيفة وقابلة للاختبار، يمكن أن تُشكّل بصمات تجريبية للديناميكيات غير الخطية أو ما بعد التحديد - دون انتهاك مُسلّمات الكم الأساسية.
قاعدة بورن - القاعدة الأساسية لميكانيكا الكم "الاحتمالية تضيف إلى 1" - لا يزال قائما على الصعيد العالمي. محلياداخل الفجوة، يمكن أن تكون استجابات الكاشف منحرف قليلا (هذه هي الفكرة)، ولكن عندما تُقيّم كل شيء بشكل صحيح، تبقى القواعد الأساسية سليمة. نحن ننحني، لا ننكسر.
تشبيه: مرآة منزل المرح التي تشوه انعكاسك في الزاوية - لكن المخطط الهيكلي للمبنى لم يتغير.
[انقر لفتح] ميزانية الإشارة:الكمية المحفوظة س_{\text{sig}} حدود قدرة الاتصال.
في وسط مُمَكَّن مثل الترانزستور المقترن الكمومي (QCT)، يمكن لتفاعلات المجال تبادل معلومات الطور عبر حاجز نفقي أسرع من الانتشار التقليدي. ومع ذلك، فإن هذا التبادل محدود بكمية قياسية محفوظة تُسمى ميزانية الإشارة، تدل عليه س_{\text{sig}}يقيس هذا المقياس إجمالي تدفق المجال المتماسك - وهو الحد الأقصى "للشحنة المعلوماتية" التي يمكن تبادلها دون انتهاك قوانين الحفاظ العالمية.
تحديد كثافة تدفق الإشارة المحلية j_{\text{sig}}^a مرتبط بتبادل المجال المتماسك الطور (مشابه لتيار الاحتمال أو الطاقة). الكمية المحفوظة الإجمالية هي س_{\text{sig}} = \int_{\Sigma_t} j_{\text{sig}}^a,u_a,d^3x, أين \سيجما_ت هي سطح فائق لوقت عالمي ثابت (شريحة التورق)، u_a هي الوحدة المحلية العمودية على تلك الشريحة (حقل متجه التورق نفسه الذي يحدد الإطار المفضل)، و j_{\text{sig}}^a يطيع معادلة الاستمرارية \nabla_a j_{\text{sig}}^a = 0. هذا يعني \frac{d Q_{\text{sig}}}{dt} = 0، so س_{\text{sig}} يتم الحفاظ عليها تحت جميع التفاعلات المحلية داخل المنطقة الممكنة.
جسديا، س_{\text{sig}} يُحدد هذا المعامل إجمالي طاقة الارتباط المتماسكة أو سعة الطور المخزنة في مجال الاقتران المتلاشي بين العقدتين (أليس وبوب). وهو ليس مطابقًا للشحنة الكهربائية أو عدد الفوتونات؛ بل يقيس الدرجة المتكاملة للتماسك المتبادل المتاحة للتعديل. لا يمكن لأي عملية اتصال سوى إعادة توزيع هذه الكمية - لا زيادتها أبدًا.
القدرة على الاتصال الكلاسيكية (شانون) C يمكن تحقيق ذلك من خلال قناة تعتمد على QCT، ويحدها دالة رتيبة لميزانية الإشارة: ج \le f(Q_{\text{sig}}), أين f(\cdot) يعتمد على هندسة الجهاز، ومعدل فقدان التماسك، والضوضاء الحرارية. بالنسبة لأنظمة الإشارات الصغيرة والاستجابة الخطية، f(Q_{\text{sig}}) \approx \frac{1}{2N_0},Q_{\text{sig}}^2, أين رقم_0 هي كثافة الطيف الضوضاء الفعالة للوصلة النفقية، مما يعطي C_{\max} \propto Q_{\text{sig}}^2. وبالتالي، فإن التدفق المتماسك الأكبر يُنتج سعة كامنة أعلى، ولكن فقط حتى النقطة التي يُكسر فيها فقدان التماسك استمرارية الطور. لنفترض وجود عقدتين من نظرية الكم الكمومي (أليس وبوب) متصلتين فقط بواسطة مجال نفقي متلاشية. لنفترض أن: \Phi_1(t) و \Phi_2(t) تكون إمكانات طورهما اللحظية. عرّف تيار الإشارة المتماسك عبر فجوة الاقتران على النحو التالي:
أين \كابا ثابت اقتران متناسب مع معامل نفق الحاجز. ميزانية الإشارة المتكاملة على فترة تماسك واحدة T_c is
يمثل هذا إجمالي التبادل المرتبط بالطور بين أليس وبوب ضمن نافذة التماسك، ويبقى ثابتًا إذا تطورت كلتا العقدتين في ظل ديناميكيات أحادية أو ضعيفة التبديد. دع I_{\text{sig}}(t) = j_{\text{sig}}(t)،A كن إشارة التيار القابلة للقياس من خلال المنطقة الفعالة A.
نسبة الإشارة إلى الضوضاء اللحظية هي \text{SNR}(t) = \frac{I_{\text{sig}}^2(t)}{N_0,B}, أين B هو عرض النطاق الترددي. التكامل عبر نافذة التماسك يعطي الحد الأقصى للسعة
جـ 1ـ 2بـ 2ـ 0ـTـcـ 0ـ 2(t)ـNـ0ـdt = أـ 2ـ 2بـ 2ـNـ0ـTـcـ jـ 2(t)ـdt.
وفقًا لنظرية بارسيفال، فإن هذا التكامل يتناسب مع س_{\text{sig}}^2، إعطاء ج \le k_B,Q_{\text{sig}}^2, أين ك_ب هو ثابت تناسب تجريبي يعتمد على الهندسة ودرجة الحرارة. على سبيل المثال العددي، لنفترض أن زوجًا من نظرية الكمومية يعمل مع اقتران الحاجز. \كابا = 10^{-3}، سعة التماسك |\Phi_1| = |\Phi_2| = 1، ووقت التماسك T_c = 10^{-12},\text{s}.
ثم Q_{\text{sig}} = \kappa \int_0^{T_c} \sin(\Delta\phi),dt \approx \kappa,T_c,\sin\langle\Delta\phi\rangle.
لمتوسط تأخر الطور \langle\دلتا\phi\rangle = \pi/4, Q_{\text{sig}} \approx 7.1\times10^{-16},\text{s}.
بدافع N_0 = 10-20,\text{J/Hz} و ب = 10^{12},\نص{هرتز}, تصبح حدود القدرة C_{\max} \approx \frac{1}{2B\ln 2}\frac{Q_{\text{sig}}^2}{N_0} \approx 3\times10^2,\text{bits/s}.
وهكذا، حتى نبضة التماسك بمقياس الفيمتوثانية قد تكون، من حيث المبدأ، قادرة على نقل معلومات منظمة قابلة للقياس ضمن حدود الحفظ الفيزيائي.
إذا كانت منطقتان اقتران موجودتان بالتوازي، فإن ميزانيات الإشارة الإجمالية الخاصة بهما تضاف خطيًا: Q_ {\ text {sig، tot}} = Q _ {\ text {sig}} ^ {(1)} + Q_ {\ text {sig}} ^ {(2)}، لكن القدرات المقابلة تضاف بشكل دون خطي بسبب التداخل: C_{\text{tot}} \le f(Q_{\text{sig,tot}}) < f(Q_{\text{sig}}^{(1)}) + f(Q_{\text{sig}}^{(2)}).[/latex] هذا يُعبّر عن قدرة التماسك المحدودة: يُمكن مشاركة التماسك، ولكن لا يُمكن تضخيمه بحرية. باختصار، [latex]Q_{\text{sig}} هو مقياس محفوظ يمثل إجمالي تدفق المجال المتماسك عبر الوسيط المُفعّل. وهو يُحدد الحد الأقصى لميزانية الاتصال للنظام. ج \le f(Q_{\text{sig}}), ضمان أن أي زيادة في القدرة القابلة للقياس تستمد من الموارد المتاحة س_{\text{sig}}يضمن المبدأ السببية والاتساق الديناميكي الحراري حتى في حالة اقتران الطور الأسرع من الضوء: يظل تبادل المعلومات محدودًا بكمية إشارة محفوظة.
نحن نعالج المتاح تماسك (الجزء المنظم من الحقل القريب في الفجوة) مثل ميزانية. يمكنك إعادة التوزيع إنها لإنشاء رسالة، ولكنك لا يمكن إنشاء المزيد من لا شيء. ميزانية أكبر ← سعر موثوق أعلى، حتى يتوقف الضجيج والحرارة.
تشبيه: بطارية لمؤشر ليزر رفيع للغاية: يمكنك وميض رمز ما، ولكن إجمالي الومضات يقتصر على البطارية.
[انقر لفتح] اللاخطية المحصورة:الأمراض التي يتم تجنبها عن طريق الحبس + حدود الطاقة.
في الأنظمة الكمومية غير الخطية أو المُختارة بعديًا، يُمكن أن تُؤدي التغذية الراجعة غير المُقيدة بين الحالة والقياس بسهولة إلى مفارقات: إشارات تفوق سرعة الضوء، أو انتهاك قاعدة بورن، أو حتى تناقضات منطقية مثل الحلقات السببية المغلقة. وللحفاظ على الاتساق الفيزيائي، يجب أن يكون أي انحراف عن التطور الكمومي الخطي مُقيدًا بدقة. حبيس - موضعية ضمن منطقة محدودة الطاقة من الزمكان، ومتصلة بالبيئة الخارجية فقط من خلال قنوات تحافظ على الوحدة الشاملة. يوفر الترانزستور المقترن كميًا (QCT) مثل هذه الحدود الطبيعية. يظهر المصطلح غير الخطي فقط ضمن الوسيط الممكّن فجوة النفق أو مجال χ - حيث يسمح اقتران الطور المتلاشي والمقاومة التفاضلية السلبية (NDR) بتفاعل ذاتي ضعيف. خارج هذه المنطقة، تسري ميكانيكا الكم الخطية القياسية تمامًا.
رسميًا، دعونا نكتب عامل تطور النظام الكامل على النحو التالي \mathcal{U}(t) = \mathcal{T}\exp!\left[-\frac{i}{\hbar}!\int (H_0 + \varepsilon,H_{\text{NL}}),dt\right], أين ح_0 هو الهاميلتوني الهيرميتي القياسي، ح_{\text{NL}} هي مساهمة غير خطية محدودة، و \varepsilon \ll 1 هي معلمة تنشيط تختفي خارج منطقة QCT. شرط الاحتجاز هو \اسم المشغل{supp}(H_{\text{NL}}) \subseteq \Omega_{\text{QCT}}، مما يعني أن التفاعل غير الخطي يقتصر مكانيًا على الوسيط الممكن \أوميغا_{\text{QCT}}. يتم الحفاظ على الوحدة العالمية إذا كان المبدل [H_{\text{NL}},H_0] يتمتع بدعم مضغوط وكثافة طاقة غير خطية
\mathcal{E} {\text{NL}} = \langle\psi|H {\text{NL}}|\psi\rangleيرضي
\mathcal{E} {\text{NL}} \le \delta E {\text{th}}،أين \delta E_{\text{th}} هو مقياس التذبذب الحراري المحلي. وهذا يضمن عدم قدرة التغذية الراجعة غير الخطية على التضخيم الذاتي بما يتجاوز حدود الضوضاء الفيزيائية.
من الناحية العملية، يعني الحبس أن الخريطة \Phi: \rho \mapsto \rho' غير خطي بشكل ضعيف فقط داخل الفضاء الفرعي الممكَّن بـχ
\mathcal{H} {\chi},بينما يظل موجبًا تمامًا ويحافظ على الأثر (CPTP) على المكمل. رياضيًا،
\Phi = \Phi {\text{CPTP}} \oplus (\Phi_{\text{CPTP}} + \varepsilon \mathcal{N})،مع \mathcal{N} يمثل التصحيح غير الخطي المحصور. لأن \varepsilon \rightarrow 0 عند حدود نظرية الكم الكمومي، لا ينتشر أيُّ عدم خطية خارج الفجوة. هذا يمنع التناقضات الشاملة ويفرض إغلاقًا سببيًا: قد توجد تأثيرات طورية تفوق سرعة الضوء ضمن التفرع المحلي، لكنها لا تُشكِّل حلقات إشارات مغلقة أو تنتشر عشوائيًا.
من الناحية الديناميكية الحرارية، يضمن حصر اللاخطية استحالة استخراج الطاقة من الفراغ. تعمل منطقة NDR النشطة كعنصر تغذية راجعة مُتحكم به، قادر على تضخيم المجالات المتلاشية، ولكن دائمًا ضمن القيد. P_{\text{out}} \le P_{\text{in}} + \Delta E_{\text{مخزن}}يتم تعويض أي مكسب مؤقت من خلال تخزين المجال المحلي، مما يحافظ على توازن الطاقة الكلي. وبالتالي، يتصرف النظام كمرنان غير خطي محصور ضمن حدود محافظة.
في إطار الإشارات الورقية السببية (CFS)، يضمن هذا الاحتواء المكاني والطاقي الاستقرار: تُعدّل الديناميكيات غير الخطية الإحصاءات المحلية دون تغيير الوحدة العالمية. يصبح QCT جزيرة غير خطية محدودة الطاقة مُضمنة في استمرارية كمية خطية.
تُستبعد تلقائيًا حالاتٌ مرضيةٌ مثل التضخيم الجامح، والحتمية الفائقة، والتغذية الراجعة اللاسببية، لأن المجال غير الخطي محدود، ومرتبطٌ بشكلٍ مُبدِّد، ومُعاد تطبيعه عالميًا. في جوهره، يعمل QCT كبيئةٍ تجريبيةٍ يُمكن أن توجد فيها لاخطيةٌ محدودة، قابلةٌ للاختبار، ولكن محصورةٌ بأمانٍ ضمن قواعد الديناميكا الحرارية الكمومية.
تعمل فجوة h-BN في QCT مثل قفص فاراداي للغرابة الكمومية صندوق رمل صغير، حيث يمكن للقواعد المعتادة أن تنحني بأمان دون أن تنكسر. داخل هذه المنطقة المعزولة، يستطيع الجهاز تضخيم الطاقة وإعادة تدويرها بما يكفي للكشف عن أنماط ضوئية خافتة، لكن حدودًا حرارية وطاقية صارمة تمنعه من التسرب.
القياس: إنه مثل بناء مضخم محمي بجدار حماية:يمكنه أن يهمس عبر الفراغ، لكنه لا يحرق أبدًا قوانين الفيزياء التي تحتويه.
[انقر لفتح] Thermo Borders (المكسب مقابل درجة حرارة الضوضاء)
كل جهاز كمي نشط مقيد في النهاية باتساق ترموديناميكي. حتى عندما يعمل الترانزستور المقترن كميًا (QCT) في نظام غير خطي أو نظام مقاومة تفاضلية سالبة (NDR)، لا يمكن أن يتجاوز كسبه الإجمالي الحد الذي تحدده درجة حرارة الضوضاء الفعالة وميزانية الإشارة المتاحة. ملزمة بالحرارة يعبر هذا الحد عن: يجب أن يطيع التضخيم ونقل التماسك في الوسط الممكن مبدأ التقلب والتبديد، مما يضمن عدم تمكن أي تكوين للجهاز من استخراج الطاقة الحرة الصافية أو انتهاك القانون الثاني.
في حالة التوازن، تكون كثافة الطاقة الطيفية للتقلبات عبر فجوة النفق هي S_V(f) = 4k_B T_{\text{eff}} R_{\text{eq}}(f)، أين ت_{\text{eff}} هي درجة الحرارة الفعالة للوصلة المقترنة و R_{\text{eq}}(f) المقاومة الديناميكية، والتي قد تصبح سالبة في ظل انحياز NDR. عندما يوفر QCT كسب إشارة صغيرة ج(ف)، تتطلب نظرية التقلب والتبديد أن يظل حاصل ضرب المكسب ودرجة حرارة الضوضاء محدودًا: G(f) T_{\text{eff}} \ge T_0, أين T_0 هي درجة الحرارة الفيزيائية للبيئة. وهذا يضمن أن أي تضخيم محلي يُدخل بالضرورة ضوضاء تعويضية، مما يُبقي توازن الإنتروبيا غير سلبي.
ينشأ النظير الكمي لهذا القيد من علاقات التبديل بين مشغلات المجال. لأي مُضخِّم يعمل على أوضاع بوزونية _hat a_{\mathrm{in}} و _hat a_{\mathrm{out}}، يجب الحفاظ على التبديل القانوني، أي
[,\hat a_{\mathrm{out}},,\hat a_{\mathrm{out}}^{\dagger},]=1.
نموذج الإدخال والإخراج القياسي غير الحساس للمرحلة هو
\ hat a _ {\mathrm {out}} = \sqrt {G}، \ hat a _ {\mathrm {in}} +\sqrt {G-1}، \ hat b _ {\ mathrm {in}} ^ {\ dagger}، \ qquad [،\ hat b _ {\ mathrm {in}}، \ hat b _ {\ mathrm {in}} ^ {\ dagger}،] = 1،
وهو ما يعني الحد الأدنى من الضوضاء المضافة.
في نظرية الكم الكمومي، تتوافق هذه الضوضاء مع المُركّب العشوائي لتيار النفق الناتج عن التقلبات الحرارية والكمية للمجال المتلاشية. يمكن كتابة مُقايضة الكسب الفعال والضوضاء على النحو التالي: G_{\text{QCT}} = 1 + \frac{P_{\text{out}} - P_{\text{in}}}{k_B T_{\text{eff}} B}، تخضع الى P_{\text{out}} \le P_{\text{in}} + k_B T_{\text{eff}} B, أين B هو عرض النطاق الترددي. يعبر هذا التفاوت عن الحد الأقصى الديناميكي الحراري للتضخيم المتماسك.
عمليًا، مع زيادة الانحياز عبر حاجز h-BN، تُمكّن منطقة NDR من إعادة حقن الطاقة في الوضع المتلاشية، مما يُضخّم المجال القريب بفعالية. ومع ذلك، فإن هذا الكسب محدود ذاتيًا: فبمجرد ارتفاع درجة حرارة الضوضاء المحلية إلى T_{\text{eff}} = T_0 + \Delta T_{\text{NDR}}، يصل النظام إلى حالة استقرار حراري. تؤدي زيادة الانحياز إلى تبديد طاقة إضافية كحرارة بدلاً من زيادة التماسك. وبالتالي، يعمل مستوى الضوضاء الحرارية كحاجز طبيعي، مما يُثبّت النظام ضد التضخيم الجامح.
وبالتالي، يمكن تلخيص الحدود الحرارية على أنها قانون حفظ يربط بين اكتساب المعلومات والمدخلات النشطة وإنتاج الإنتروبيا: \Delta I \le \frac{\Delta E}{k_B T_{\text{eff}} \ln 2}. إن عدم المساواة هذا يحدد الكفاءة النهائية لأي قناة اتصال تعتمد على نظرية الكم الكمومي أو تجربة إشارات مقسمة سببيًا: فمعدل المعلومات الذي يمكن تحقيقه لكل وحدة إنفاق طاقة لا يمكن أن يتجاوز تكلفة إنتروبيا الحفاظ على التماسك.
من منظور أوسع، يُعدّ الحد الحراري النظير الحراري لقيود ميزانية الإشارة. بينما س_{\text{sig}} حدود التدفق المتماسك الإجمالي، ت_{\text{eff}} يُحدد هذان العاملان التضخيم القابل للاستخدام ضمن هذا التدفق. ويُعرّفان معًا نافذة التشغيل لنظرية الكم الكمومي كنظام رنيني كمي ولكنه مغلق ترموديناميكيًا. لا تُولّد أو تُفقد أي طاقة تتجاوز التبادل المسموح به مع البيئة، ويظل التغير الإجمالي في الإنتروبيا غير سلبي. \frac{dS_{\text{tot}}}{dt} = \frac{P_{\text{in}} - P_{\text{out}}}{T_0} \ge 0.
في الأساس، يضمن Thermo Bound أن QCT يعمل كـ مضخم كمي متوافق مع الديناميكية الحرارية - قادرة على تحقيق مكسب متماسك الطور واقتران أسرع من الضوء داخل منطقتها الممكنة، ولكنها مقيدة دائمًا بتوازن الطاقة والإنتروبيا الأساسي الذي يحافظ على السببية العالمية والقانون الفيزيائي.
إذا حاولت تضخيم المجال القريب في الفجوة، فإنك ترفعه أيضًا درجة حرارة الضوضاء الفعالةهناك معادلة: زيادة المكسب تعني ضوضاء أكثر. تُطبّق الطبيعة هذا التوازن حتى... لا يمكن احصل على طاقة مجانية أو تضخيم غير محدود وواضح للغاية.
تشبيه: رفع صوت الجيتار: إشارة أعلى، ولكن أيضًا هسيسًا أكثر. في مرحلة ما، يُضيف الصوت العالي ضوضاءً وحرارةً.
[انقر لفتح] النموذج الأدنى: ديناميكيات الكاشف/المضخم غير الخطية في الوسائط الممكّنة
في المناطق المُمكّنة، مثل حاجز نفق QCT، نفترض وجود عدم خطية ضعيفة تعتمد على الحالة في خريطة القياس أو التضخيم. هذه الخريطة، المُشار إليها بـ ن_{\تشي}، تعمل على مصفوفة الكثافة المحلية \rho من النظام الفرعي المقترن بحقل الإشارة \تشيإنه يحافظ على الاحتمالية الكلية (الحفاظ على الأثر) ولكنه يقدم عدم خطية متحكم بها كافية لإنتاج سعة كلاسيكية محدودة، وإن كانت صغيرة.
1. فريف
N_{\chi}(\rho) = \frac{A_{\chi} \rho A_{\chi}^{\dagger}}{\mathrm{Tr}(A_{\chi} \rho A_{\chi}^{\dagger})}،
أين A_{\chi} = I + \epsilon, F(\rho, \chi) هو عامل غير خطي يعتمد بشكل ضعيف على مجال الإشارة \تشي وعلى حالة النظام الحالية \rho. المعلمة الصغيرة \إبسيلون \ll 1 يتحكم في درجة اللاخطية.
التطبيع في المقام يفرض \mathrm{Tr[N_{\chi}(\rho)] = 1، والتأكد من أن الخريطة تحافظ على الآثار ومتسقة فعليًا.
2. الحد الخطي
متى \ إبسيلون = 0، يتم تقليص النموذج إلى القياس الكمي القياسي:
N_{\chi}(\rho) \to \rho' = \frac{M \rho M^{\dagger}}{\mathrm{Tr}(M \rho M^{\dagger})},
أين M هو عامل القياس (عنصر POVM).
وبالتالي، فإن النموذج غير الخطي هو امتداد بسيط لميكانيكا الكم القياسية.
3. الديناميكيات الفعالة
بالنسبة للخطية الضعيفة، تحفز الخريطة معادلة تطور فعالة:
\dot{\rho} = -\frac{i}{\hbar}[H, \rho] + \epsilon, \mathcal{L} {\chi}[\rho],أين
\mathcal{L} {\chi}[\rho]يمثل اقترانًا وظيفيًا غير خطي لحالة النظام بحقل الإشارة.
يمكن صياغة هذا المصطلح ظاهريًا على النحو التالي:
\mathcal{L}_{\chi}[\rho] = f(\chi),(\rho^2 - \rho,\mathrm{Tr[\rho^2]),
إدخال مكسب أو توهين يعتمد على الحالة ويختفي بالنسبة للحالات النقية (\rho^2 = \rho).
4. سعة المعلومات
النتيجة الرئيسية هي أن الكشف غير الخطي أو الذي تم اختياره لاحقًا يمكن أن ينتج عنه سعة كلاسيكية صغيرة ولكنها محدودة ج_{\mathrm{eff}} عبر ما قد يكون بخلاف ذلك قناة للتشابك فقط (بدون إشارات):
C_{\mathrm{eff}} \approx p_{W}, C,
أين ص_{و} هو احتمال نجاح نافذة ما بعد الاختيار غير الخطية، و C هي سعة قناة الإشارة المثالية.
يتوافق هذا مع انحراف طفيف ولكن قابل للقياس عن سلوك عدم الاتصال الصارم في الوسائط الممكنة:
C_ {\mathrm{eff}} > 0، \qquad C_{\mathrm{eff}} \ll C_{\mathrm{classical}}.5. مثال فيزيائي: اقتران حاجز QCT
في الترانزستور المقترن الكمي، تعمل طبقتا الجرافين ككاشفات متماسكة محليًا متصلة عبر حاجز كمي.
مجال الإشارة الفعال \chi(t) يمثل إمكانات الطور التلاشي عبر منطقة نفق h-BN.
تدخل اللاخطية من خلال شفافية الحاجز المعتمد على الجهد:
T_{\chi}(V) = T_{0} \exp[-\alpha (1 - \beta V + \epsilon, \Phi_{\chi}(\rho))],
أين \Phi_{\chi}(\rho) هو مصطلح ردود فعل ضعيفة يربط تماسك الدالة الموجية المحلية بحالة المجال.
تعمل هذه التغذية الراجعة على تعديل احتمالية النفق غير محليًا ولكنها تحافظ على الوحدة العالمية.
6. الحفظ والاستقرار
ولمنع التضخيم الجامح، فإن المصطلح غير الخطي يلبي قيد الحفاظ:
\mathrm{Tr[\rho,\mathcal{L}_{\chi}[\rho]] = 0،
ضمان بقاء الاحتمالية الكلية والطاقة ثابتة إلى الدرجة الأولى في \epsilon.
يؤدي هذا إلى إبقاء الديناميكيات متسقة ومحدودة - وتجنب المفارقات الأسرع من الضوء مع السماح بنقل الإشارة المتماسكة التي لا يمكن ملاحظتها.
7. ترجمة
والنتيجة هي قاعدة الكم المعدلة بشكل طفيف:
استجابة الكاشف غير خطية إلى حد ما وتعتمد على الحالة، مما يخلق انحرافًا صغيرًا عن نظرية عدم الاتصال الصارمة مع الاحتفاظ بتطبيع قاعدة بورن عالميًا.
في المناطق الممكنة (على سبيل المثال، حقول حاجز h-BN، ودوائر التزامن المختارة لاحقًا)، يتصرف التفاعل كما لو كانت معلومات الطور قادرة على النفق عبر الفراغ الكمومي - حاملة إشارة كلاسيكية صغيرة ومحدودة عبر فصل يشبه الفضاء، دون كسر الوحدة أو السببية العالمية.
كان ليست إعادة كتابة ميكانيكا الكم في كل مكان. نضيف التواء صغير يعتمد على الحالة لكيفية استجابة الكاشف/المضخم داخل الفجوة - بما يكفي للسماح بنمط خافت يتأثر بالضوضاء. خارج الفجوة، كل شيء عادي وخطي. داخلها، تكون الاستجابة قليلا مدرك للسياق (هذا هو الجزء "غير الخطي")، ونحن نحافظ عليه المحصورة لذلك لا شيء يهرب.
تشبيه: ميكروفون مزود بضاغط مدمج خفي لا ينشط إلا في نقطة صغيرة حلوة - في معظم الأحيان يكون شفافًا، ولكن في تلك النقطة يشكل الإشارة بما يكفي لسماعها.
4. التنبؤات التجريبية
- تباين الإطار المعتدل: تعتمد سرعة الإشارة على المحاذاة مع يو
- التحويل المتلاشي → الانتشاري تحت تعديل تحيز QCT
- التي تسيطر عليها انتهاك حدود تسيريلسون
- قياس التأخير مع تحيز الوصلة، وليس سمك الحاجز
5. بروتوكولات الاختبار
- اختبار QCT ثنائي المختبر: يؤدي تعديل التحيز عند العقدة A إلى إحداث استجابة مترابطة عند العقدة B خارج المخروط الضوئي.
- تبديل الإطار المتحرك: يتم تكرار ذلك في الحركة النسبية لاختبار محاذاة الإطار المفضل.
- الحقنة الزائلة: موجه موجي أقل من القطع متصل بفجوة QCT للكشف عن الاسترداد المعدل بالطور.
6. دور فريق الجودة
يؤدي نفق الفيمتوثانية لـ QCT وسلوك NDR إلى خلق عدم خطية محصورة ضرورية لـ تماسك تفوق سرعة الضوء يمكن التحكم فيه. يتم الحفاظ على السببية من خلال قيد عدم وجود حلقة، مما يضمن النظام العالمي.

في الخلاصة: يحافظ نموذج CFS على النسبية في كل مكان تقريبًا، مع السماح بمخروط إشارة منظم نشط فقط في وسائط كمية محددة مثل QCT. يقدم هذا الإطار تنبؤات قابلة للاختبار للتواصل الأسرع من الضوء ولكن المتسق سببيًا.
هذه المقالة جزء من سلسلة تتعلق برؤية غير مفسرة رأيتها في أيرلندا عام 1986:
- جسم غامض فوق خليج جالواي الفصل الأول: لقاء سالثيل عام 1986
- تقرير الأجسام الطائرة المجهولة السوداء:الأمير تشارلز، وطائرة جامبو، وليلة من الألغاز الجوية
- جسم غامض فوق خليج جالواي الفصل الثاني: استغاثة نفسية من جسم غامض تحطم
- جسم غامض فوق خليج جالواي الفصل الثاني: الأيرلنديون Tuatha Dé Danann كزوار كونيين
- جسم غامض فوق خليج جالواي الفصل الأول: الهندسة العكسية للترانزستور المقترن الكمومي
- الترانزستور المقترن الكمي (QCT): تضخيم الفراغ
- هل يمكن للمعلومات أن تنتقل أسرع من الضوء؟ - بدون كسر الفيزياء؟